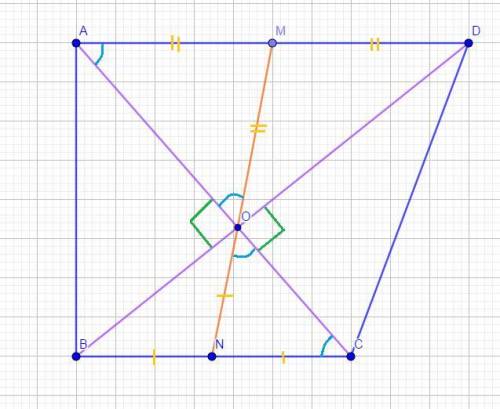
Четырехугольник ABCD, O - точка пересечения диагоналей,
AD || BC и AC ⊥BD,
M - середина AD, N - середина BC,
AD = 12 и BC = 7 (смотрите рисунок).
Найти:Длина отрезка MN.
Решение:Заметим, что O ∈ MN, так как угол MON - развернутый:
∠MON = ∠DOC + (∠DOM + ∠CON) = 90° + (∠OCB + ∠OBC) =
= 90° + 90° = 180°.
Значит, нам достаточно найти длину MO + NO.
Так как треугольник AOD прямоугольный, то медиана MO, проведенная из вершины прямого угла к гипотенузе, равна половине этой гипотенузы (по свойству медианы прямоугольного треугольника):
MO = AD / 2 = 12 / 2 = 6.
Тоже самое можно сказать и о прямоугольном треугольнике BOC с медианой NO:
NO = BC / 2 = 7 / 2 = 3,5.
Значит:
MO + NO = MN = 6 + 3,5 = 9,5.
ответ:MN = 9,5 .
Четырехугольник ABCD, O - точка пересечения диагоналей,
AD || BC и AC ⊥BD,
M - середина AD, N - середина BC,
AD = 12 и BC = 7 (смотрите рисунок).
Найти:Длина отрезка MN.
Решение:Заметим, что O ∈ MN, так как угол MON - развернутый:
∠MON = ∠DOC + (∠DOM + ∠CON) = 90° + (∠OCB + ∠OBC) =
= 90° + 90° = 180°.
Значит, нам достаточно найти длину MO + NO.
Так как треугольник AOD прямоугольный, то медиана MO, проведенная из вершины прямого угла к гипотенузе, равна половине этой гипотенузы (по свойству медианы прямоугольного треугольника):
MO = AD / 2 = 12 / 2 = 6.
Тоже самое можно сказать и о прямоугольном треугольнике BOC с медианой NO:
NO = BC / 2 = 7 / 2 = 3,5.
Значит:
MO + NO = MN = 6 + 3,5 = 9,5.
ответ:MN = 9,5 .

опускаем высоту из вершины. получаем прямоугольный треугольник со стороной 10 и 6 (т.к. трапеция равнобедренная 12/2=6). по теореме пифагора находим второй катет, который является так же высотой трапеции. он равен 8.
рассматриваем другой прямоугольный треугольник - где высота это катет, а диагональ - гипотенуза. по теореме пофигора находим там второй катет, который является оставшимся куском основания. он получается 15.
дальше. маленькое основание будет равно (15+6)-12=9
площадь трапеции = полусумма оснований на высоту = (21+9)/2*8=96