Ромб - стороны равны, противоположные углы равны, диагонали перпендикулярны.
Треугольники ABE и CBF равны по гипотенузе и острому углу, AE=CF.
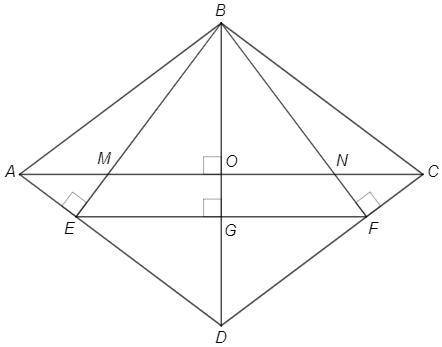
Точки E и F делят стороны ромба в равном отношении => AC||EF => EF⊥BD
S(ABO) =1/4 S(ABCD) =1/4 *1/2 *160*120 =2400
AB =√(AO^2 +BO^2) =100
∠ABD=∠ADB => △ABO~△BDE
BE/AO =BD/AB => BE =80*120/100 =96
△BEG~△BMO~△BDE => △BEG~△BMO~△ABO
S(BEG)/S(ABO) =(BE/AB)^2 =(96/100)^2 =0,96^2
S(BMO)/S(ABO) =(BO/AO)^2 =(60/80)^2 =0,75^2
S(MOGE) =S(BEG)-S(BMO) =2400 (0,96^2 -0,75^2) =861,84
S(MNFE) =2 S(MOGE) =1723,68
Задача на подобие треугольников и теоремы о параллельных плоскостях и прямых.
Проведем через точку М, А2 и В2 плоскость.
А1В1 параллельна А2В2 как линии пересечения параллельных плоскостей третьей плоскостью.
Остюда треугольники МА2В2 и МА1В1 подобны.
Примем отрезок МВ1 за х
Тогда МВ2=9+х,
МА2=9+х+4
4:(13+х)=х:(9+х)
36+4х=13х+х²
х²+9х-36=0
При необходимости полное решение квадратного уравнения запишете самостоятельно, а корни его 3 и -12. Второй корень не подходит.
х=3 см
МВ2=9+3=12 см
МА2=12+4=16 см