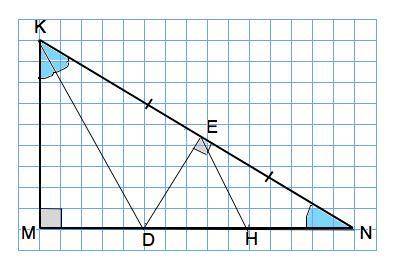
В ∆ KDN отрезок DE - высота, а т.к. KЕ=EN, то и медиана.
Следовательно, ∆ KDN - равнобедренный, углы DKN=KND.
Угол NKD= углу MKD Поэтому угол МКN=2 угла N.
Сумма острых углов прямоугольного треугольника 90°.
3N=90° => Угол N=30°.
В прямоугольном ∆ DЕN проведем медиану ЕН.
По свойству медианы прямоугольного треугольника ЕН=DH=HN, треугольник ЕНN и треугольник DEH- равнобедренные. Угол HED=ЕDN=90°-30°=60°, ∆ DEH – равносторонний.
Точка D по свойству биссектрисы равноудалена от сторон КМ и КN.
МD=DE, а DE=DH=HN => MD=HN => MN=3MD. Доказано.
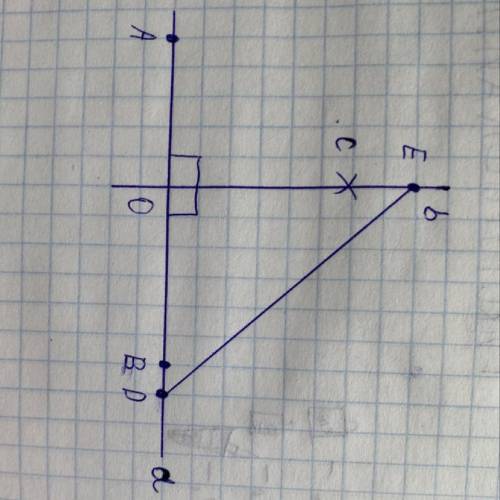
∠CAD = ∠BDA, ⇒ ΔAOD равнобедренный.
ΔAOD подобен ΔСОВ по двум углам (углы при вершине О равны как вертикальные, ∠OAD = ∠ОСВ как накрест лежащие) ⇒ ΔСОВ тоже равнобедренный.
Проведем высоту трапеции КН через точку пересечения диагоналей.
Тогда, ОН - высота и медиана равнобедренного прямоугольного ΔAOD, а медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине.
ОН = AD/2
Аналогично, ОК - высота и медиана ΔВОС,
ОК = ВС/2
КН = (AD + BC)/2 = 4 см, т.к. полусумма оснований - это средняя линия.
Стоит запомнить это свойство: в равнобедренной трапеции с перпендикулярными диагоналями высота равна средней линии.