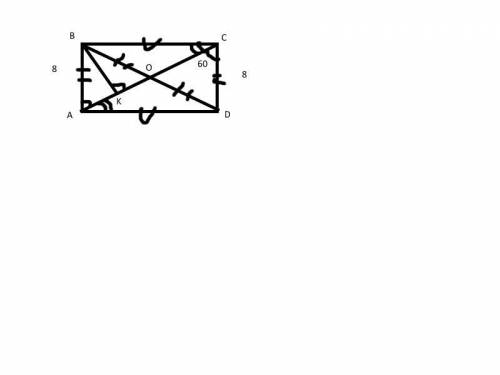
Дано: ABCD - прямоугольник
BK⊥AC
∠ACD=60°
AB=8 см
Найти: BD = ?
OK = ?
Т.к ABCD - прямоугольник, то AB=CD=8 см
∠OCD=∠BAO (н/л BC || AD и сек. AC) = 60°
∠BCO=∠OAD (н/л) = 90-60=30°
В прямоугольном ΔABC, ∠B=90°, ∠ACB=30°. Напротив угла в 30° в прямоугольном Δ лежит катет, равный половине гипотенузы => AB=0,5*AC => 8=0,5*AC => AC=8:0,5 => AC=16
Диагонали в прямоугольнике точкой пересечения делятся пополам => AO=OC=8 см.
ΔOCD - р/б т.к OC=CD => ∠COD=∠ODC. Сумма углов в треугольнике равна 180° => ∠COD=∠ODC= (180°-60°)/2=60° => ΔOCD - равносторонний по признаку => OD=OC=CD=8 см
BO=OD (диагональ делится пополам точкой пересечения)
BD=2*OD
BD=2*8
BD=16 см
ΔBOA - равносторонний (AB=BO=AO=8 см) => BK - высота, биссектриса и медиана => OK= 0,5*AO; OK=0,5*8; OK=4
ответ: BD = 16 см; OK = 4 см
Объяснение:
Добавлю "дурацкое алгебраическое" решение.
Пусть боковая сторона треугольника AB=BC=c, тогда AC =2c cos 40° (для упрощения писанины обозначение градуса буду опускать),
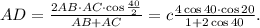
При этом 
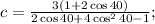

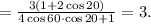
Мы воспользовались известными (как мне кажется) в школе формулами для длины биссектрисы через прилежащие стороны и угол, а также для длины отрезка стороны, на которую опущена биссектриса.
Возможно, приведет к успеху и другой путь - в этой задаче возникают углы в 60 (угол ADB) и 120 (соответственно угол ADC) градусов, поэтому можно написать хорошие тождества, скрепляющие элементы чертежа. При этом полезно провести биссектрису DF=BD угла ADC и достроить до ромба. Правда, с первого захода довести до ответе этот путь не удалось.
