Диагональ делит прямоугольник на два равных прямоугольных треугольника. Рассмотрим ΔАСD (см. прикрепленный рисунок).
АС является гипотенузой в ΔАСD. АС = 3. Также известен острый угол в этом треугольнике ∠CAD = 37°.
Через синус и косинус найдем катеты треугольника АСD.
Синус острого угла в прямоугольном треугольнике - отношение противолежащего катета к гипотенузе.
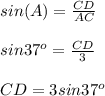
Косинус острого угла в прямоугольном треугольнике - отношение прилежащего катета к гипотенузе.
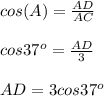
CD и AD являются шириной и длиной в прямоугольника АВСD.
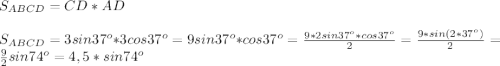
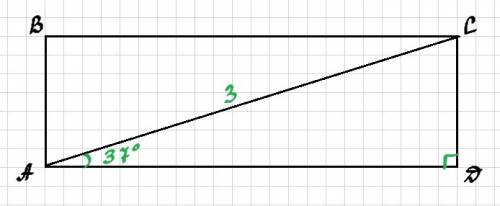
ответ: 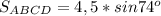 см².
см².
дан паралелограмм абсд с высотой бк и <бак=60, бс = 6. полощадь пар-ма=бс*бк.
30 корней из 3 = 6*бк . бк= 5 корней из 3. Рассмотри треугольник абк- он прямоугольный. аб= бк / sin60= 5 корней из 3/ корень из 3/2 = 10. перимитр- 2*6 + 2*10=32