...
Объяснение:
ПУсть угол 1=39°, тогда угол 3=141°.
Угол 2(который обозначен красной ручкой) и угол 3 вертикальные. Значит угол 2=углу 3=141°
Если прямые б и е параллельные, то отсюда следует, что угол 1 и угол 2 односторонние углы и их сумма должна равняться 180°, если же сумма односторонних углов не будет равна 180°, то прямые не параллельные.
Проверка:
Угол 1+угол 2=180°; 39°+141°=180°; 180°=180°.
Значит эти прямые параллельные.
К этому я прикрепила рисунок, чтобы вы не перепутались где какие углы и решение тоже там.

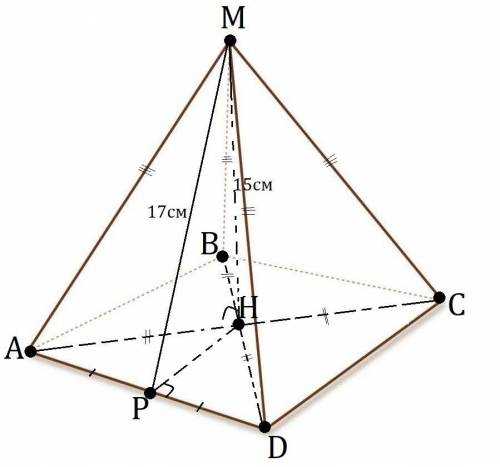
В правильной пирамиде высота падает в центр основания, то есть в центр правильного многоугольника. Правильный четырёхугольник это квадрат, а его центр находится на пересечении диагоналей. Боковые грани правильной пирамиды это равнобедренные треугольники, которые равны. Апофема это высота боковой грани. В квадрате все стороны равны, диагонали равны и делятся точкой пересечения пополам.
Пусть P∈AD и MP⊥AD, тогда MP=17см и AP=PD т.к. в равнобедренном Δ высота является и медианой.
Пусть H∈(ABC) и MH⊥(ABC), тогда AC∩BD=H.
ΔMHP - прямоугольный, найдём неизвестный катет.
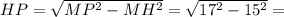
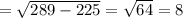 см.
см.
ΔAHD - равнобедренный, поэтому PH не только медиана, но и высота.
ΔHPD - прямоугольный, ∠HDP=45° т.к. диагонали квадрата являются и биссектрисами, значит HP=PD=8см - равны как катеты, прямоугольного Δ с острым углом в 45°.
AD=2·PD=2·8см=16см.
Площадь квадрата можно найти через сторону, а площадь равнобедренного треугольника через сторону и высоту опущенную на эту сторону.
S(ABCD) = AD²=16² см².
S(AMD) = MP·AD:2=17·16:2 см².
S(бок. пов.) = 4·S(AMD)=4·17·16:2 см²=2·17·16 см².
S(полн. пов.) = S(ABCD)+S(бок. пов.) = 16²см²+2·17·16 см² = 32·(8+17)см² = 8·4·25см²=800см².
ответ: 800см².
В прямоугольном треугольнике против угла в 30 ° лежит катет, равны половине гипотенузы
Н=2√3
(2R)²=(4√3)²-(2√3)²=48-12=36=6² ⇒ 2R=6 ⇒ R=3
V(цилиндра)=πR²·H=π·36·(2√3)=72π·√3 куб. см
2
Высота равнобедренного треугольника ( сечения конуса) является его медианой и биссектрисой. В прямоугольном треугольнике против угла в 30° лежит катет, равный половине гипотенузы
R=L/2=3 cм
S(бок)=πR·L=π·3·6=18π кв см
3.
По теореме Пифагора находим хорду АВ
АВ²=17²-15²=289-225=64=8²
АВ=8
В равнобедренном треугольнике АОВ высота, проведенная из точки О служит расстоянием между осью цилиндра и сечением, проведенным чере хорду АВ.
Высота равнобедренного треугольника является и медианой, высота разделила треугольник АОВ на два прямоугольных треугольника с гипотенузами 5 и одним катетом 4, второй катет 3 ( треугольник египетский)
ответ. 3 см