Есть два решения этой задачи - стандартное и на сообразительность.
Начну со второго. Учитывая, что расстояние между домами равно сумме высот дома и фонаря, нужного результата мы добьемся, если рассыпем зёрна на расстоянии 6 метров от дома. Тогда катеты левого прямоугольного треугольника равны 8 и 6 метров, правого - 6 и 14-6=8 метров. То есть эти треугольники равны, а тогда у них равны гипотенузы, чего и нужно было добиться.
Первый Если расстояние от первого дома равно x, то квадрат гипотенузы левого треугольника равен 8²+x², а квадрат гипотенузы правого треугольника равен 6²+(14-x)²; а поскольку гипотенузы по условию должны быть равны, получаем уравнение
64+x²=36+196-28x+x²; 28x=168; x=6
Объяснение:
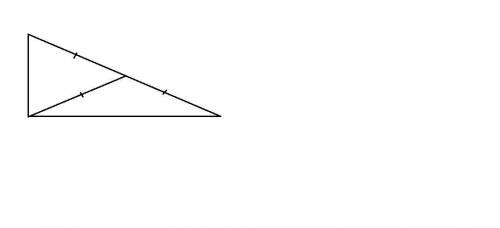
а) Любой прямоугольный треугольник можно разрезать на два равнобедренных треугольника.
Верно.
В любом прямоугольном треугольнике медиана, проведенная к гипотенузе, равна ее половине (см. рисунок). Если разрезать треугольник по медиане, то получим два равнобедренных треугольника.
б) Существует четырехугольник со сторонами 2, 3, 5, 11.
Неверно.
Каждая сторона четырехугольника должна быть меньше суммы остальных его сторон.
В данном четырехугольнике для стороны 11:
11 < 5 + 3 + 2 - неравенство неверно, значит четырехугольник с такими сторонами не существует.
в) В любом выпуклом пятиугольнике всегда есть тупой угол.
Верно.
Сумма углов выпуклого многоугольника определяется по формуле:
180°(n - 2), где n - количество сторон.
Для пятиугольника:
180° · 3 = 540°.
Если предположить, что все его углы острые (меньше 90°), то сумма будет меньше 90° · 5 = 450°. Значит есть тупой угол.
г) Внутри любого треугольника существует точка, равноудаленная от всех его вершин.
Неверно.
Точка, равноудаленная от всех вершин треугольника, - это центр описанной окружности.
Только в остроугольном треугольнике центр описанной окружности лежит внутри треугольника. В прямоугольном - на стороне (середина гипотенузы). В тупоугольном - вне треугольника.