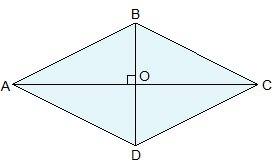
Тетраэдр это многоугольник состоящий из 4 граней, для решения задачи необходимо, чтобы все его рёбра были равны или какое-то ещё дополнительное условие, иначе для решения задачи не хватает данных.
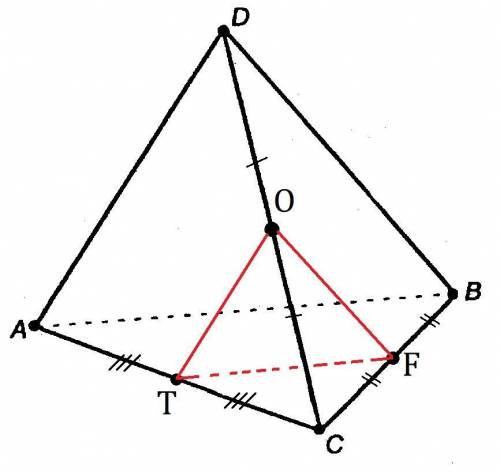
F, O, T - середины ребер BC, DC, AC соответственно. Поэтому FO, OT, TF - средние линии треугольников CBD, CDA, CAB соответственно. А значит, BD=2FO, DA=2OT, AB=2TF.
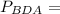BD+DA+AB = 2FO+2OT+2TF = 2(FO+OT+TF) = 
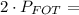2·12см = 24см.
ΔBDA - равносторонний (все рёбра тетраэдра равны), поэтому BD=DA=AB=24см:3=8см. Найдём площадь равностороннего треугольника по формуле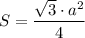 
, где a - сторона треугольника.
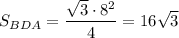см².
Площадью боковой поверхности, будет площадь любых 3 граней (все грани это равные, равносторонние треугольники).
S(бок.) =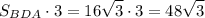 
см².
ответ: 48√3 см².
Диагонали делят ромб на 4 равных прямоугольных треугольника с катетами 6 см и 8 см.
По теореме Пифагора
a²=(d₁/2)²+(d₂/2)²=6²+8²=100
a=10