Площадь боковой поверхности правильной шестиугольной пирамиды равна площади 6-ти равнобедренных треугольников с основанием, равным стороне основания пирамиды и высотой, равной апофеме.
Т.е.
Площадь боковой поверхности правильной шестиугольной пирамиды равна половние произведения апофемы на периметр основания.
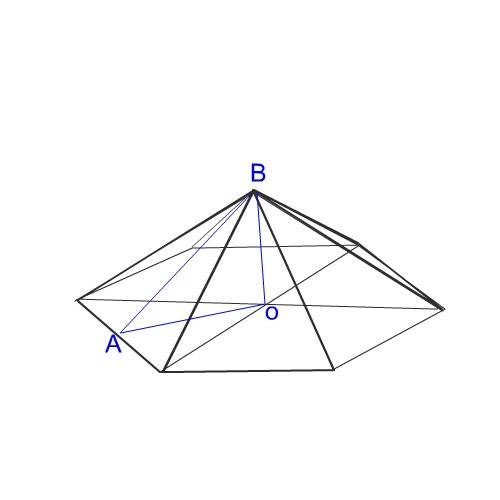
Апофему найдем из треугольника АВО, где ВО - высота пирамиды, АО- радиус вписанной в шестиугольник окружности. Он равен высоте равностороннего треугольника, из которых состоит основание.
ВО=2,
АО==а(√3):2=4(√3):2=2√3
Апофема
АВ=√(АО²+ВО²)=√16=4
S бок=6·4·4:2=48 см²
Так как длины сторон четырёхугольника пропорциональны числам 2 : 3 : 4 : 5, то пусть их длины равны соответственно 2х, 3х, 4х, 5х (х — коэффициент пропорциональности).
Периметр — это сумма длин всех сторон.Следовательно :
2х + 3х + 4х + 5х = 56 см
14х = 56 см
х = 56 см : 14
х = 4 см.
2х = 2*4 см = 8 см.
2х = 2*4 см = 8 см.3х = 3*4 см = 12 см.
2х = 2*4 см = 8 см.3х = 3*4 см = 12 см.4х = 4*4 см = 16 см.
2х = 2*4 см = 8 см.3х = 3*4 см = 12 см.4х = 4*4 см = 16 см.5х = 5*4 см = 20 см.
ответ : 8 см, 12 см, 16 см, 20 см.
На сторонах кута А відкладені відрізки АВ=4см, ВС=5см, АD=6см, DE=2см. Знайдіть відношення площ трикутника ABD і чотирикутника BCED.На сторонах кута А відкладені відрізки АВ=4см, ВС=5см, АD=6см, DE=2см. Знайдіть відношення площ трикутника ABD і чотирикутника BCED.На сторонах кута А відкладені відрізки АВ=4см, ВС=5см, АD=6см, DE=2см. Знайдіть відношення площ трикутника ABD і чотирикутника BCED.На сторонах кута А відкладені відрізки АВ=4см, ВС=5см, АD=6см, DE=2см. Знайдіть відношення площ трикутника ABD і чотирикутника BCED.На сторонах кута А відкладені відрізки АВ=4см, ВС=5см, АD=6см, DE=2см. Знайдіть відношення площ трикутника ABD і чотирикутника BCED.На сторонах кута А відкладені відрізки АВ=4см, ВС=5см, АD=6см, DE=2см. Знайдіть відношення площ трикутника ABD і чотирикутника BCED.
Объяснение:
h=2sqrt(3) высота основания
l=sqrt(4*3+4)=4 -апофема
S=6*4*4/2=16*3=48