2) Прямая призма состоит из 6 поверхностей: двух совершенно одинаковых оснований и 3-х боковых сторон. Самое простое сначала вычислить площадь основания призмы. Так как это прямоугольный треугольник, то вычисляется по формуле половина произведения его катетов. То есть 0,5*3*4=6 см. Каждая боковая сторона вычисляется отдельно как площадь прямоугольника. Площадь AA1B1B равняется произведению высоты призмы на сторону AB. 4*10=40 см2. Площадь BB1CC1 равна произведению стороны BC на высоту призмы, то есть 3*10=30 см2. Чтобы вычислить сторону призмы ACC1A1 над вычислить по теореме Пифагора сторону AC. 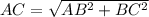
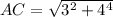 . AC=5 см. Значит площадь третьей боковой стороны равна произведению высоты призмы на сторону AC. 5*10=50 см2. Значит площадь всей поверхности призмы равна
. AC=5 см. Значит площадь третьей боковой стороны равна произведению высоты призмы на сторону AC. 5*10=50 см2. Значит площадь всей поверхности призмы равна

 S=132 cм2.
S=132 cм2.
1) Площадь поверности октаэдра состоит из 8 равносторонних треугольников. Достаточновычислить площадь одного из равносторонних треугольников и помножить все то на 8. Так как сторона одного из этих треугольников равна 1 см, то, вспомнив, что в равностороннем треугольнике все углы равны и они по 60 градусов каждый, то можно вычислить с формулы  , где
, где  - угол между сторонами a и b. Значит
- угол между сторонами a и b. Значит  .
. 
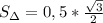 . Теперь умножим эту площадь на 8. Получим
. Теперь умножим эту площадь на 8. Получим 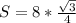
 .
.

Объяснение:
№3
r=S/p (S-площадь p-полупериметр)
p=1/2(AB+AC+BC)=1/2(25+7+24)=28
S=1/2*AC*BC=1/2*7*24=84
r=84/28=3
ответ: 3
№4
Найдем сторону AB по теореме синусов:
AB/ sin90=AC/sin30
AB/1=10/0.5
AB=20
AO=OB (так как радиусы окружности), поэтому
AO=1/2AB=1/2*20=10
ответ: 10
№6
Проведем в треугольнике АВС высоту ВВ1, треугольник АВВ1- прямоугольный
АВ1=АО=7(радиусы окружности)
Треугольник АВС равнобедренный, значит ВВ1 это и биссектриса угла АВС
Рассмотрим треугольник АВВ1:
Найдем сторону АВ по теореме синусов:
АВ/sin 90= AC/sin 60
AB/1=7/ (корень из 3)/2
АВ=(14 корней из трех)/2
ответ: (14 корней из трех)/2
ответ: 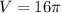 см³.
см³.
Объяснение:
Дано:
Равнобедренный треугольник вращается вокруг высоты.
Высота проведена к основанию равнобедренного треугольника.
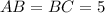 см.
см.
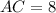 см.
см.
-----------------------------------------------
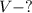
При вращении равнобедренного треугольника вокруг высоты, образовался конус. Значит нам нужно найти объём конуса.
Высота 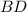 является по свойству равнобедренного треугольника медианой и биссектрисой
является по свойству равнобедренного треугольника медианой и биссектрисой 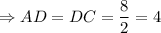 см.
см.
Теперь найдём высоту 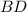 по теореме Пифагора (
по теореме Пифагора (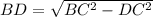 , где
, где 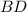 и
и 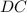 - катеты,
- катеты, 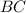 - гипотенуза):
- гипотенуза):
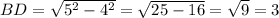 см.
см.
Затем найдём объём образовавшегося конуса:
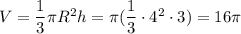 см³.
см³.
2) c^2=9+16=25 c=5
S=3*4+10*(3+4+5)=12+120=132
1) 8*(1*1/2)*sqrt(3)/2=2sqrt(3)