Раз отрезок д.б. параллелен оси абсцисс, то координаты Y точек M и N должны быть одинаковыми:
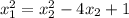
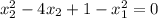
Решим относительно 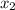
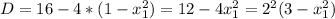
Для того, что бы такие точки существовали, нужно 
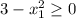
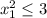
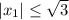
С другой стороны, т.к. длина отрезка MN д.б. равна 3, то:
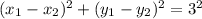
Координаты 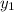 и
и 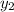 , как мы уже выяснили равны, т.о.:
, как мы уже выяснили равны, т.о.:
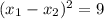
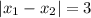
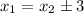
Подставим это в имеющееся уравнение 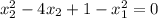 :
:
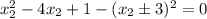
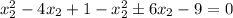


Следовательно: 
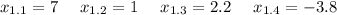
Среди них только 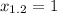 удовлетворяет условию
удовлетворяет условию 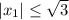
Т.о. координаты точки M(1;1) и точки N(4;1)
Рисунок: http://yotx.ru/default.aspx?clr0=000000&exp0=x%5e2&clr1=666666&exp1=x%5e2-4x%2b1&clr2=ff0000&pv2=on&pt2=%281%3b1%29%284%3b1%29&mix=-10&max=10&asx=on&u=mm&nx=x&aiy=on&asy=on&ny=y&iw=600&ih=400&ict=png&aa=on
Объяснение:
1. Сумма углов выпуклого многоугольника равна 180°*(n-1), где n -
количество углов выпуклого многоугольника.
S=180°*(7-2)=180°*5=900°.
2. S=6*7=42 (cм²).
3. S=180°*(13-2)=180°*11=1980°.
4. 15*7=105 (cм²).
5. S=ah/2 h=2S/a=2*45/18=90/18=5 (cм).
6. (1/2) основания = √(15²-9²)=√(225-81)=√144=12 (см).
S=12*9=108 (cм²).
7. Пусть меньшая диагональ - х. ⇒
Большая диагональ - х+8.
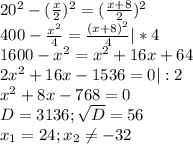
24+8=32 (см). ⇒
S=(24*32)/2=12*32=384 (cм²).
8. S=10*9,5=95 (дм²) s=0,5²=0,25 (дм²) ⇒
N=95/0,25=380 (квадратов).
y=x^2
y=x^2-4x+1
Точка М принадлежит параболе y=x^2, значит M(a;a^2)
Точка N принадлежит параболе y=x^2-4x+1, значит N(b;b^2-4b+1)
Т.к. отрезок MN параллелен оси Ох, то ординаты точек M и N должны быть равны.
a^2=b^2-4b+1
По условию, расстояние MN=3, значит b-a=3
b=a+3
Подставим это значение b в наше уравнение:
a^2=(a+3)^2-4(a+3)+1
a^2=a^2+6a+9-4a-12+1
2a-2=0
2a=2
a=1
b=a+3=1+3=4
M(1;1), N(4;1)
Теперь осталось построить в одной координатной плоскости две параболы
y=x^2 и y=x^2-4x+1, на первой отметить точку M, а на второй точку N и провести отрезок MN.