1)Суммы противоположных сторон четырехугольника в который можно вписать окружность равны.Значит можно найти боковые стороны: 100:2=50 -сумма боковых сторон. 50:2=25 - боковая сторона.
2)a+b=50 - cумма оснований .из этой формулы найдем ср. линию:(a+b):2=25
3)Диаметр(высота) окружности (трапеции) =2r=2*12=24
4)Найдем площадь:
S=(a+b)/2*h=25*24=600 cм^2
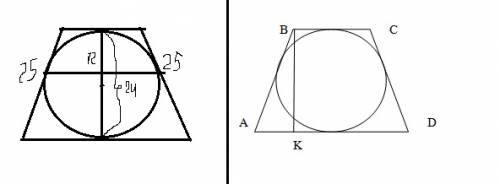
5)Посчитаем больщее основание по теореме Пифагора(см. второй рисунок)
AB^2=BK^2+AK^2
25^2=24^2+AK^2
AK=7
BC=AD-2AK=AD-14
Подставим в формулу:BC+AD=50
AD-14+AD=50
2AD=64
AD=32
6)Найдем меньшее основание:
50-32=18
ответ:a=18 ; b=32 ; S=600
Объяснение:
Сначала найдем стороны параллелограмма
( 5 + 6 ) * 2 = 22 части приходится на все четыре стороны параллелограмма
44 \ 22 = 2 см - приходится на одну часть
2 * 5 = 10 см - ширина параллелограмма
2 * 6 = 12 см - длина параллелограмма
cos A = АН \ АВ = АН : 10
Составляем пропорцию и решаем ее
3 : 5
АН : 10
АН = 3 * 10 \ 5 = 6 см
По теореме Пифагора находим высоту - ВН
ВН = √АВ² - АН² = √100 - 36 =√64 = 8 см
Для нахождения площади трапеции нам нужно знать длину обоих оснований
НD = 12 - 6 = 6 см длина нижнего основания трапеции
( ВС + НD) \ 2 * ВН = ( 12 + 6 ) \ 2 * 8 = 72 см² - площадь трапеции НВСD
1,5*(7+2√2) см.
Объяснение:
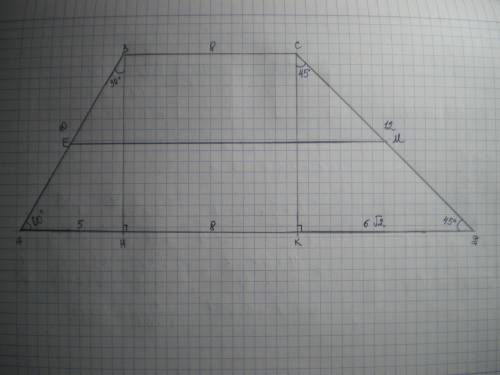
Дано: АВСD - трапеция, ∠А=60°, ∠D=45°, АВ=10 см, СD=12 см, ВС=8 см.
ЕМ - средняя линия. Найти ЕМ.
Проведем высоты ВН и СК.
ΔАВН - прямоугольный, ∠А=60°, тогда ∠АВН=90-60=30°, а АН=1/2 АВ по свойству катета, лежащего против угла 30 градусов
АН=10:2=5 см
ΔКDС - прямоугольный, ∠D=45°, ∠DСК=90-45=45°, значит КD=СК
Пусть КD=СК=х см, тогда по теореме Пифагора х²+х²=12²
2х²=144; х²=72; х=√72=6√2 см.
КD=СК=6√2 см.
АD=АН+КН+КD=5+8+6√2=13+6√2 см.
ЕМ=(ВС+АD):2=(8+13+6√2):2=(21+6√2):2=1,5*(7+2√2) см.
Около окружности можно описать трапецию тогда и только тогда, когда равны суммы ее противоположных сторон.
Следовательно, сумма оснований равна сумме боковых сторон и равна полупериметру трапеции.
Сумма оснований равна 100:2=50 см
Трапеция равнобокая, и каждая боковая сторона равна
50:2=25 см
Площадь трапеции равна произведению ее высоты на полусумму оснований.
Высота трапеции равна диаметру окружности, вокруг которой она описана, и равна r·2=12·2=24cм.
S=24·50:2=600 см²
Теперь найдем основания.
Проведем из вершины тупого угла высоту к большему основанию.
Высота отсекает от него отрезок, равный полуразности оснований. Обозначим его х.
Из прямоугольного треугольника, в котором боковая сторона трапеции - гипотенуза, а катеты - высота и отрезок х, найдем х.
х=√(25²-24²)=√49=7 см
Так как х- это полуразность оснований, то полная разность 7·2=14 см.
Сумма оснований 50. Пусть меньшее из них будет у, тогда большее у+14
у+у+14=50
2у=36
у=18 - это меньшее основание.
18+14=32 - это большее основание.
ответ:
Меньшее основание =18 см
Большее основание =32 см
Площадь трапеции =600 см