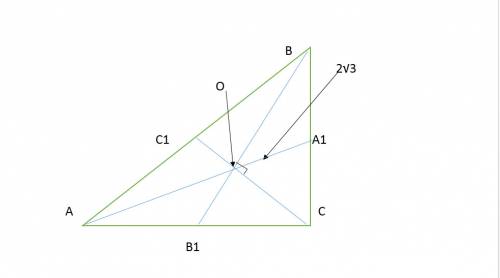
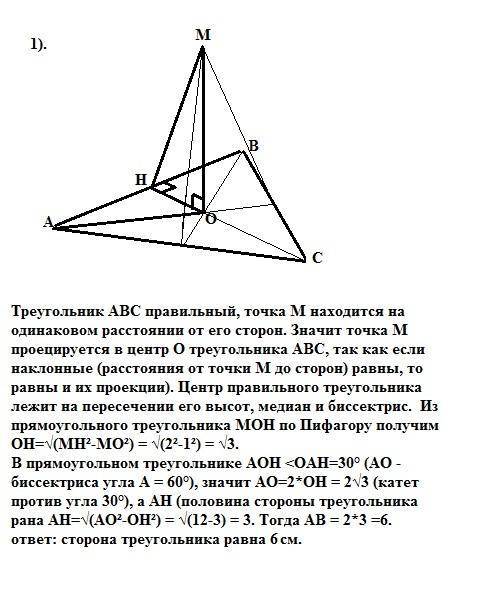
1). Треугольник АВС правильный, точка М находится на одинаковом расстоянии от его сторон. Значит точка М проецируется в центр О треугольника АВС, так как если наклонные (расстояния от точки М до сторон) равны, то равны и их проекции). Центр правильного треугольника лежит на пересечении его высот, медиан и биссектрис. Из прямоугольного треугольника МОН по Пифагору получим
ОН=√(МН²-МО²) = √(2²-1²) = √3см.
В прямоугольном треугольнике АОН <OAH=30° (АО - биссектриса угла А = 60°), значит АО=2*ОН = 2√3 (катет против угла 30°), а АН (половина стороны треугольника рана АН=√(АО²-ОН²) = √(12-3) = 3см.
Тогда АВ = 2*3 =6см.
ответ: сторона треугольника равна 6 см.
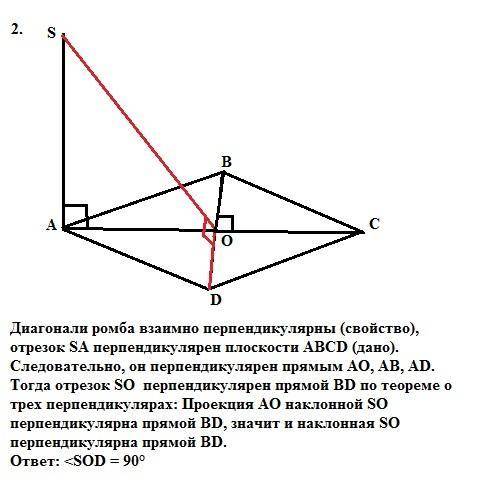
2). Диагонали ромба взаимно перпендикулярны (свойство), отрезок SA перпендикулярен плоскости АВСD (дано). Следовательно, он перпендикулярен прямым АО, АВ, AD.
Тогда отрезок SO перпендикулярен прямой BD по теореме о трех перпендикулярах: Проекция AO наклонной SO перпендикулярна прямой BD, значит и наклонная SO перпендикулярна прямой BD.
ответ: <SOD = 90°.
Найти: угол АВК
Решение:
Т.к. ΔАВС - равнобедренный, то угол С= углу В = 70 градусов, тогда
по теореме о сумме углов треугольника угол А = 180-(70*2)=40 градусов;
угол АКВ равен 90 градусов, так как он смежен с прямым углом ВКС,
аналогично по теореме о сумме углов треугольника угол АВК = 180-(90+40)=180-130=50 градусов
ответ: 50 градусов