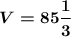куб. ед.
Объяснение:
Пирамида правильная, значит основание - квадрат, а высота проецируется в точку пересечения диагоналей квадрата.
Н - середина CD, тогда SH - апофема пирамиды.
SH = 4√2
SH⊥CD, OH - проекция SH на плоскость основания, значит ОН⊥CD по теореме, обратной теореме о трех перпендикулярах.
∠SHO = 45° - линейный угол двугранного угла при ребре основания.
Рассмотрим ΔSOH:
∠SOH = 90°, ∠SHO = 45°, ⇒ ∠HSO = 45°, треугольник равнобедренный.
SO = OH = x
По теореме Пифагора:
SH² = SO² + OH²
(4√2)² = x² + x²
2x² = 32
x² = 16
x = 4 (x = - 4 не подходит по смыслу задачи)
SO = 4 - высота пирамиды
AD = 2OH = 2 · 4 = 8, так как ОН - средняя линия треугольника ACD.
Sabcd = AD² = 8² = 64
Объем пирамиды:
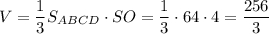
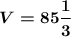
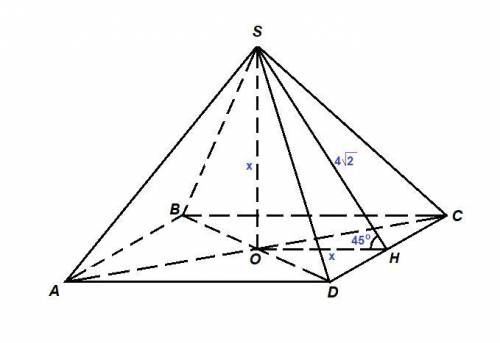
объем = V=a⋅b⋅h=10⋅24⋅10=2400см3
Объяснение:
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Длина и ширина нам известны, необходимо вычислить высоту.
Площадь диагонального сечения равна произведению диагонали основания и высоты прямоугольного параллелепипеда.
S(диаг. сеч.)=c⋅h=a2+b2−−−−−−√⋅h=102+242−−−−−−−−√⋅h=676−−−√⋅h=26⋅h.
По условию задачи площадь диагонального сечения прямоугольного параллелепипеда равна 260см2.
26⋅h=260
h=26026=10см
Вычислим объем
V=a⋅b⋅h=10⋅24⋅10=2400см3
