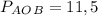см
∠AOB=90°
∠ABO=50°
∠BAO=40°
Объяснение:
Дано: ABCD - ромб
CD = 3 см
AC = 9 см
BD = 8 см
∠C = 80°
Найти: PΔ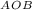
= ?
∠AOB=?
∠ABO=?
∠BAO=?
Решение: т.к ABCD - ромб, то у него все стороны равны ⇒ CD=BC=AB=AD=3 см
Диагонали ромба точкой пересечения делятся пополам: BO=OD=8/2=4 см; AO=OC=9/2=4,5 см
Противолежащие углы ромба равны ⇒ ∠C=∠A=80°, но т.к диагонали ромба являются биссектрисами его углов, то ∠OAD=∠BAO=80/2=40°
Диагонали ромба пересекаются под прямым углом ⇒ ∠AOB=90°
В ΔABO - прямоугольном, найдем ∠ABO. Сумма острых углов в прямоугольном треугольнике = 90°
∠ABO+∠BAO=90; ∠ABO=90-∠BAO; ∠ABO=90-40; ∠ABO=50°
Периметр - сумма длин всех сторон, тогда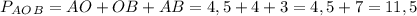 
см
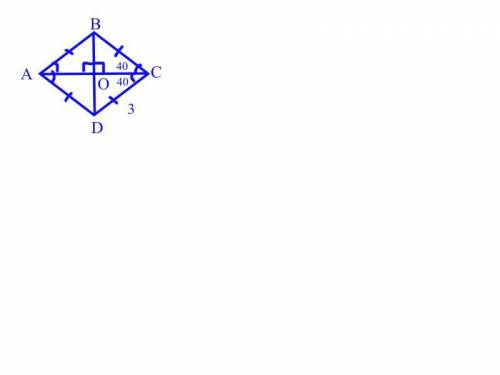
Радиус окружности, описанной около равнобедренного треугольника с углом 120°, равен см. Найдите стороны треугольника
Объяснение:
ΔАВС, ∠В=120°, О-центр описанной окружности. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров к его сторонам.
Пусть ВН⊥АС, О∈ВН., ОВ=ОА=6√3 см.
По теореме синусов( отношение стороны треугольника к синусу противолежащего угла равно двум радиусам описанной окружности) :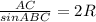 
, 
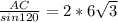, АС=12√3*
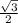=18 (см).
По свойству высоты равнобедренного треугольника ∠АВН=∠НВС=60°, АН=НС=9 см.
ΔАВН-прямоугольный , sin 60°=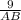
, АВ=6√3 см ⇒ВС=6√3 см.
3x=15
x=5 боковые стороны
5+1=6 основание
6/2=3 половина основания
v(5^2-3^2)=v(25-9)=v16=4 высота