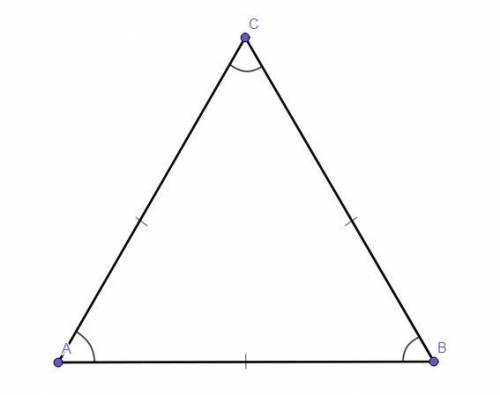
ΔАВС - равносторонний.
Доказать :∠А = ∠В = ∠С.
Доказательство :По определению равностороннего треугольника -
АВ = ВС = АС.
по свойству равнобедренного треугольника).Так как АВ = ВС, то ΔАВС - равнобедренный.
Углы у основания равнобедренного треугольника равны.Следовательно -
∠С = ∠А.
Но также АВ = АС.
Поэтому -
∠С = ∠В.
Теперь рассмотрим данное соотношение -
∠С = ∠А
∠С = ∠В
Отсюда следует, что -
∠А = ∠В = ∠С.
по соотношениям между сторонами и углами в треугольнике).Чем больше/меньше сторона в одном треугольнике, тем больше/меньше противолежащий угол в этом треугольнике.Не сложно догадаться, что -
Если в одном треугольнике равны стороны, то напротив этих сторон лежат равные углы.Так как -
АВ = ВС = АС
То и -
∠А = ∠В = ∠С.
- - -Что требовалось доказать!
р=(5+6+7)/2=9 м
S=7·h/2
6√6=7·h/2 ⇒ h=12√6/7
R=a·b·c/4S
R=(5·6·7)/(4·6√6)=35/(4√6)
По теореме косинусов
6²=5²+7²-2·5·7·сosω ( ω- угол против стороны 6)
сosω=19/35
Медиана, проведенная к стороне 7, делит эту сторону пополам
По теореме косинусов из треугольника со сторонам 5; 3,5 и медианой m
m²=5²+3,5²-2·5·3,5·cos ω
m²=25+12,25-35·cosω
m²=25+12,25-35·(19/35)
m²=18,25
m=√73/2