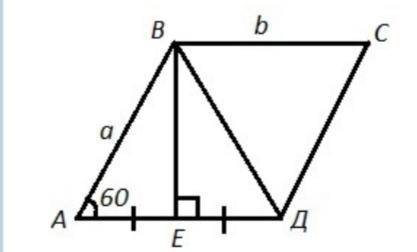
Объяснение:АВСД - параллелограмм , ∠А=60° , Р=48 см , ВЕ⊥АД , АЕ=ЕД .
Периметр параллелограмма Р=2·(a+b)=48 ⇒ a+b=24 .
АД+АВ=24 см.
Так как ВЕ - высота и АЕ=ЕД , то ΔАВД - равнобедренный: АВ=ВД .
Так как в равнобедренном ΔАВС один из углов равен 60°, то ΔАВС - равносторонний ⇒ АВ=ВД=АД ⇒ АД+АВ=2·АВ=24 , АВ=24:2=12 .
Диагональ ВД=АВ=12АВСД - параллелограмм , ∠А=60° , Р=48 см , ВЕ⊥АД , АЕ=ЕД .
Периметр параллелограмма Р=2·(a+b)=48 ⇒ a+b=24 .
АД+АВ=24 см.
Так как ВЕ - высота и АЕ=ЕД , то ΔАВД - равнобедренный: АВ=ВД .
Так как в равнобедренном ΔАВС один из углов равен 60°, то ΔАВС - равносторонний ⇒ АВ=ВД=АД ⇒ АД+АВ=2·АВ=24 , АВ=24:2=12 .
Диагональ ВД=АВ=12 см
Cоставим сначала уравнение плоскости, проходящей через ось ОУ и точку М(5,3,2).
Так как ось ОУ принадлежит искомой плоскости α, то любая точка, лежащая на оси ОУ, принадлежит плоскости α . В том числе и начало координат, точка О(0,0,0) ∈α .
Так как точка М(5,3,2)∈α , то и вектор ОМ∈α . Координаты вектора ОМ=(5,3,2) .
Также единичный вектор оси ОУ, вектор j=(0,1,0) , принадлежит плоскости α .
Можем записать нормальный вектор искомой плоскости α как векторное произведение векторов ОМ и j .
![\vec{n}=\Big [\, \overline {OM}\, ,\; \vec{j}\, \Big ]=\left|\begin{array}{ccc}\vec{i}&\vec{j}&\vec{k}\\5&3&2\\0&1&0\end{array}\right|=-2\vec{i}+5\vec{k}\\\\\\\lambda =-1\; \; \Rightarrow \; \; \; \; \vec{n}_1=\lambda \vec{n}=(2,0,-5)\\\\\alpha :\; \; A(x-x_0)+B(y-y_0)+C(z-z_0)=0\\\\2\cdot (x-5)+0\cdot (y-3)-5\cdot (z-2)=0\\\\\boxed {\alpha :\; \; 2x-5z=0}](/tpl/images/1007/7246/0300b.png)
Общие уравнения прямой, образованной пересечением двух заданных плоскостей имеют вид:
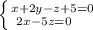
В=45⁰
значит треугольник авс равнобедренный, т.к углы при основании равны(угол А= углу В)
значит стороны АС и СВ равны( по свойству р/б треугольника)
пусть сторона АС и СВ=х
тогда по теореме пифагора
х²+х²=16²
2х²=256
х= √128
Sтреуг=АС*АВ/2
S= √128*√128/2=128/2=64
ответ:64