Объем пирамиды = V = S осн · H / 3
1) найдем H: так как sina = противолежащий катет / на гипотенузу
находим H = sina·L.
2) найти R описанной окружности основания..т.е 2h/3..R= cosa·L=2h/3 = h = (3 cos a · L)/2..
треугольника..a(квадрат)а(квадрат)/4 = h(квадрат)..a = (3 cos a ·L) / корень из 3...подставляем под формулу для вычисления площади треугольника = a ((квадрат) корень из 3 )/4 ..получаем S = 3 cos(квадрат) A · L(квадрат) · корень из 3 / и все деленное 4..теперь все подставляем в формулу V для объема..
V = 3 · Cos(квадрат) А · sin A · L (куб)· корень из 3 и все деленное на 4

Средняя линия MK = (AD + NC)/2 = (16 + 5)/2 = 21/2 = 10,5 см
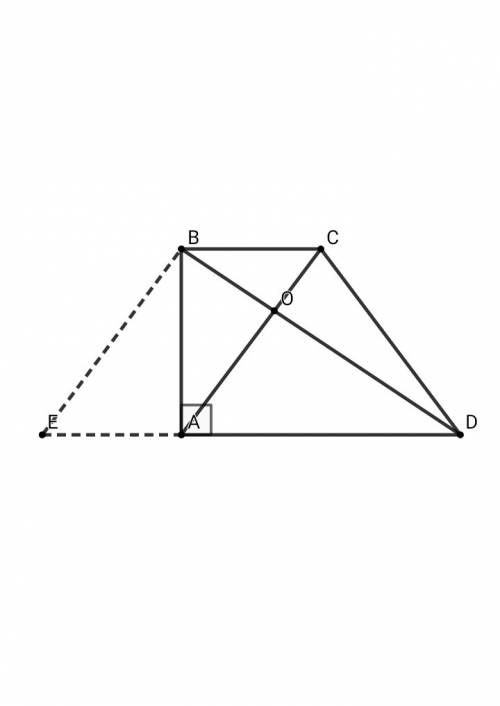
2) Угол NAB = NAD = a, BCD = BAD = 2a, ABC = ADC = 180 - 2a
У трапеции ANCD сумма углов 360
ANC = 360 - NAD - NCD - ADC = 360 - a - 2a - 180 + 2a = 180 - a
ANB = 180 - ANC = a = NAD.
Треугольник NAD - равнобедренный, у него два угла равны.
AB = CD = BN = 11 см
Периметр P(ABCD) = 2*11 + 2(11+5) = 22 + 32 = 54 см.