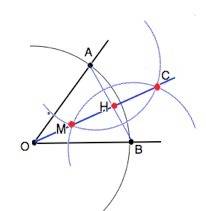
Ставим ножку циркуля в вершину О угла и проводим полуокружность, пересекающую стороны угла в т.А и В.
ОА=ОВ=R. Соединим точки А и В. Треугольник АОВ равнобедренный.
Из т. А и В как из центра раствором циркуля R больше половины расстояния АВ проводим полуокружности.
Точки их пересечения и вершина угла лежат на одной прямой. Соединяем их.
Для окружностей МС - общая хорда, АВ соединяет их радиусы. АВ и МС взаимно перпендикулярны (свойство).⇒ ОН - высота равнобедренного треугольника, следовательно, по свойству высоты равнобедренного треугольника она же – его биссектриса. Биссектриса ОС построена.
Задача имеет решение только если эта фигура – четырехугольник, вписанный в окружность.
В противном случае величину углов АDC и DCB вычислить невозможно, они могут принимать различное значения, лишь бы их сумма была равна разности между суммой углов четырехугольника и суммой углов АВС и BAD, т.е. 204°
-----------
Четырехугольник можно вписать в окружность, если сумма его противолежащих углов равна 180º.
Тогда ∠ADC=180°-∠ABC=180°-96=84°
∠BCD=180°-∠BAD=180°-60°=120°⇒
∠BCD-∠ADC=120°-84°=36°.