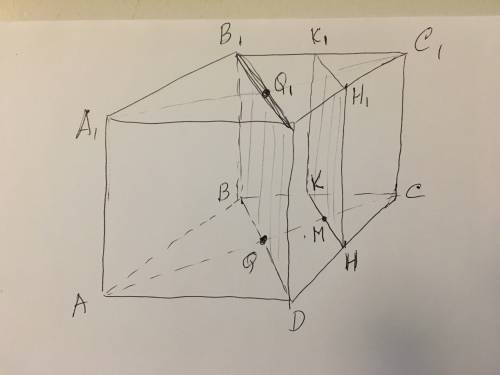
Построим сечение куба плоскостью проходящей через точки H (середина стороны DC), H1 (середина стороны D1C1) и M (середина отрезка CQ)
Соединим H с H1, продолжим отрезок HM до пересечения со стороной BC в точке K. Рассмотрев ΔBCD, видим, что отрезок HM проходит через середины стороны CD и высоты CQ, а следовательно KM является средней линией ΔBCD. Тогда K - середина стороны BC. Т.к. A1B1C1D1 || ABCD, то плоскость KHH1 пересекает их по параллельным прямым. Прямая параллельная KH и принадлежащая плоскости A1B1C1D1 и проходящая через точку H1 также будет средней линией K1H1, но в ΔC1B1D1.
Окончательно получаем в сечении прямоугольник KHH1K1.
Теперь построим сечение проходящее через точки Q, Q1 и D1
Проводим прямую через точки Q1 и D1 в плоскости A1B1C1D1 - это будет диагональ B1D1. Проводим прямую параллельную ей и принадлежащую плоскости ABCD и проходящую через точку Q - это будет диагональ BD. Окончательно получаем в сечении прямоугольник BDD1B1
BD || KH (KH - средняя линия ΔBCD)
BB1 || KK1 (KK1 - средняя линия квадрата BB1C1C)
BD пересекается с BB1 в точке B
KH пересекается с KK1 в точке K
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны ⇒ BDD1B1 || KHH1K1.
В параллелограмме смежные углы равны 180’ —> если угол АВС = 150’, угол ВАС = 30’
Из точки В проведём высоту к АD - BH. Получается прямоугольный треугольник с углами 30’, 90’, 60’ (180’-90’-30’)
А в таких треугольниках катет на против угла 30’ равен половине гипотенузе, которая в данном треугольнике равна 8см —> ВН = 4см.
Площадь параллелограмма равна 1/2(AD*BH) = 1/2(10см*4см) = 40см^2(сантиметров в квадрате)
Периметр равен сумме всех сторон, так как в параллелограмме противоположные стороны равны, P = 10см + 8см + 10см + 8см = 36 см
ответ: S=40см^2, P=36см
Пусть х - один из катетов, тогда y - второй катет. Используя теорему Пифагора, составим систему уравнений:
13=√(х²+у²)
13+2=√((х+4)²+у²)
13=√(х²+у²)
15=√((х+4)²+у²)
Возуведем обе части в квадрат, чтобы избавиться от корня:
169=х²+у²
225=(х+4)²+у²
169=х²+у²
225=х²+8х+16+у²
Из первого уравнения выразим х:
169=х²+у²
х²=169-у²
х=√(169-у²)
Теперь подставим выражение √(169-у²) вместо х во второе уравнение:
225=х²+8х+16+у²
225=(√(169-у²))²+8(√(169-у²))+16+у²
225=169-у²+8√(169-у²)+16+у²
225-169-16=8√(169-у²)
40=8√(169-у²)
40:8=√(169-у²)
5=√(169-у²) - возведем обе части в квадрат.
25=169-у²
у²=169-25
у²=144
у=√144
у=12 см - первый катет.
Если у=12, то х=√(169-у²)=√(169-12²)=√(169-144)=√25=5 см - второй катет.
ответ: катеты равны 5 и 12 см.