Question

На завтра надо! желательно полное решение. буду . три металлических кубика с ребром а сплавлены в один шар. что больше: площадь поверхности этого шара или суммарная площадь поверхности кубиков?

Answer 1

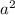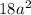
Суммарная площадь поверхности кубиков: 3 * 6 * $a^2$ = $18a^2$

Объём шара равен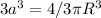 $3a^3 = 4/3 \pi R^3$. Потому радиус шара равен $R = \sqrt[3]{\frac3{2\pi}}a$. Следовательно, площадь поверхности шара равна $4 \pi R^2 = 4 \pi (\sqrt[3]{\frac3{2\pi}}a)^2 = a^2 \cdot \sqrt[3]{\frac{ 9 {\pi}^2}{32}} \approx 1.4 a^2 < 18a^2$

Потому площадь суммарная площадь поверхности кубиков больше.