
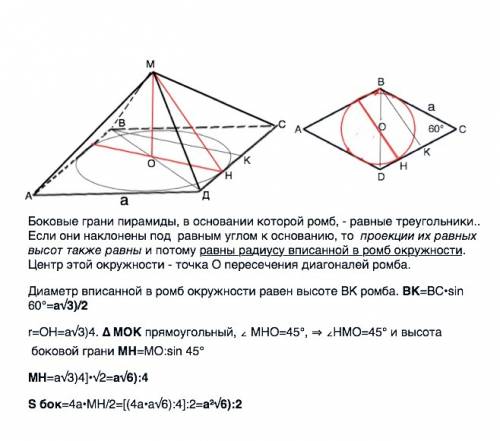
Боковые грани пирамиды, в основании которой ромб, - равные треугольники.. Если они наклонены под равным углом к основанию, то проекции их равных высот также равны и потому равны радиусу вписанной в ромб окружности. Центр этой окружности - точка О пересечения диагоналей ромба.
Диаметр вписанной в ромб окружности равен высоте ВК ромба. ВК=ВС•sin 60°=a√3)/2
r=ОН=a√3)4. ∆ МОК прямоугольный, ∠ МНО=45°, ⇒ ∠НМО=45° и высота боковой грани МН=МО:sin 45°
МН=a√3)4]•√2=a√6):4
S бок=4а•MH/2=[(4a•a√6):4]:2=a²√6):2
arccos(1/3) ~ 70.