Задача решена Пользователем Рисадес Хорошист
Исправлена неточность в последнем действии.
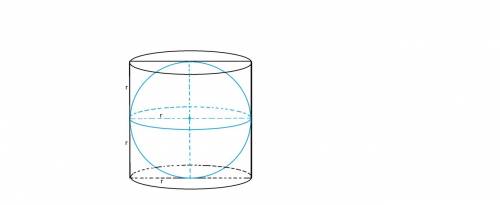
Шар может быть вписан в цилиндр только тогда, когда этот цилиндр правильный, т.е. когда его осевое сечение является квадратом.
Радиус основания цилиндра равен радиусу шара и равен r.
Высота цилиндра равна диаметру основания и равна 2 r.
Полная площадь поверхности складывается из площади двух оснований и площади боковой поверхности:
2*πr² + 2πr*2r = 6πr²
Площадь шара = 4πr²
Площадь цилиндра больше площади шара в
6πr² : 4πr² = 1,5 (раза)
Площадь полной поверхности шара
111 : 1,5 = 74 ( единиц площади)
1) По рисунку видно, что диагонали прям-ка равны диаметру вписанной окр-ти, значит радиус этой окр-ти равен половине диагонали прям-ка.
2)Так как площадь прям-ка равна произведению его длины на ширину, то 2х=8, где х - вторая сторона прям-ка, которая равна 8/2=4 см.
3) Диагональ АС прям-ка АВСД вычислим по теореме Пифагора из прямоугольного тр-ка АСД с прямым углом Д: АС=sqrt(2^2+4^2)=sqrt(20)=2*sqrt(5).
4) r=0,5*AC=sqrt(5)