рис 379: из треугольника АВС по теореме Пифагора
АВ²=ВС²+АС²=36+64=100
АВ=±√100=±10 -10 не удовлетворяет условию задачи
ответ 10
рис380:из треугольника АВС по теореме Пифагора
АС²=АВ²+ВС²
ВС²=АС²-АВ²=(7-5)(7+5)=2*12=24
ВС=±√24=±2√6. -2√6 не удовлетворяет условию задачи
ответ 2√6
рис381: из треугольника DВА по теореме Пифагора
АВ²=ВD²+АD²
АD²=АВ²-ВС²=(13-12)(13+12)=25
AD=±√25=±5. -5 не удовлетворяет условию задачи
АС=АD*2=10
ответ 10
рис382: из треугольника АОD по теореме Пифагора
АD²=AO²+OD²=(√5)²+2=5+2=7
AD=±√7. -√7 не удовлетворяет условию задачи
АD=ВС(АВСD-ромб)
ВС=√7
ответ√7
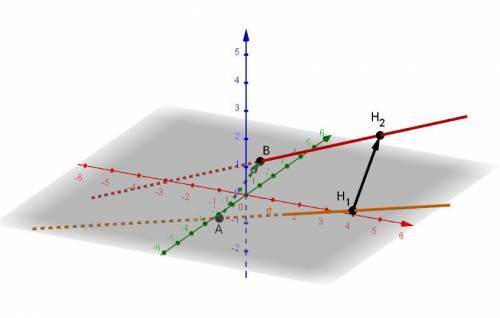
Даны уравнения прямых:
(x + 1)/3 = y/(-1) = (z + 1)/(-1) и (x + 1)/2 = (y - 3)/(-1) = z/1 .
1) Перепишем уравнения первой прямой в параметрической форме:
x = 3t - 1,
y = -t,
z = t - 1.
Примем точку Н1 как точку пересечения первой заданной прямой и общего перпендикуляра.
Её координатам соответствует вполне конкретное значение параметра, обозначим его через to . Тогда координаты точки запишутся в виде:
x = 3to - 1,
y = -to,
z = to - 1.
Аналогично для точки Н2 получим
x = 2so - 1,
y = -so + 3,
z = -so.
2) Находим вектор Н1Н2 по двум принципам.
Н1Н2 = p как результат векторного произведения направляющих векторов заданных прямых (ведь он перпендикулярен обеим прямым).
i j k | i j
3 -1 1 | 3 -1
2 -1 1 | 2 -1 = -1i + 2j - 3k -3j + 1i + 2k = 0i - 1j - 1k.
p = (0; -1; -1).
С другой стороны, вектор Н1Н2 проходит через 2 точки, координаты которых заданы в пункте 1.
Н1Н2: (2so - 3to; -so + to + 3; so - to + 1).
Поскольку направляющие векторы коллинеарны, то один вектор линейно выражается через другой с некоторым коэффициентом пропорциональности «лямбда»:
(2so - 3to; -so + to + 3; so - to + 1) = λ(0; -1; -1).
Или покоординатно:
2so - 3to = λ*0;
-so + to + 3 = λ*(-1);
so - to + 1 = λ*(-1)
Получилась самая, что ни на есть обычная система линейных уравнений с тремя неизвестными , которая стандартно разрешима, например, методом Крамера.
so to λ B
2 -3 0 0 Определитель -2
-1 1 1 -3
1 -1 1 -1
Заменяем 1-й столбец на вектор результатов B:
0 -3 0
-3 1 1 Определитель -6
-1 -1 1
Заменяем 2-й столбец на вектор результатов B:
2 0 0
-1 -3 1 Определитель -4
1 -1 1
Заменяем 3-й столбец на вектор результатов B:
2 -3 0
-1 1 -3 Определитель 4
1 -1 -1
so= -6/ -2 = 3
to= -4/ -2 = 2
λ= 4/ -2 = -2.
Отсюда находим координаты точек:
Н1 = (5; -2; 1) и Н2 = )5; 0; 3).
Вектор Н1Н2 = (0; 2; 2) и его длина √(0²+ 2² + 2²) = √8 = 2√2.
произведение полу-периметра на радиус вписанной окружности
или
половину произведения двух сторон на синус угла между ними))
отрезки касательных, проведенных из одной точки (из вершины треугольника)) равны...
центр вписанной окружности лежит на пересечении биссектрис углов))
радиус в точку касания перпендикулярен касательной...
приравняв две формулы для площади, можно найти радиус...