Тут нужно считать через подобие треугольников: ∆АВЕподобен∆СВD
АВ/ВС=ВЕ/ВD=AE/CD=2/1,(т.к. СD средняя линия треугольника, то она будет равна половине основания АЕ, угол ВАЕ=ВСD, BDC=BEA) коэффициент подобия мы нашли, он равен 2(если бы мы делили наоборот ВD/ВЕ,тогда он был бы равен 1/2), Далее нужно знать, что отношение площадей малого треугольника ВСD и большого треугольника BAE равно квадрату коэффициента подобия, т.е.
S(это площадь)∆ВСD/S∆BAE=1/4(потому что мы 1/2 возвели в квадрат, если бы мы делили эти площади наоборот, тогда приравнивали бы к 4/1)
Ну а дальше пропорцией решаем:
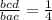
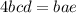
ВАЕ=12(по условию), тогда
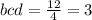
Вот и ответ: S∆BCD=3 см^2
ах+by+c=0
Для построения прямой достаточно двух точек:
при х=0 -9у-18=0 у=-2
при у=0 2х-18=0 х=9
Прямая проходит через точки
(0;-2) и (9;0)