Подробное решение во вложенном файле. ответы округлены с точностью до десятых. Заранее извиняюсь за неровный рисунок (он в принципе понятный).............................................................................................................................

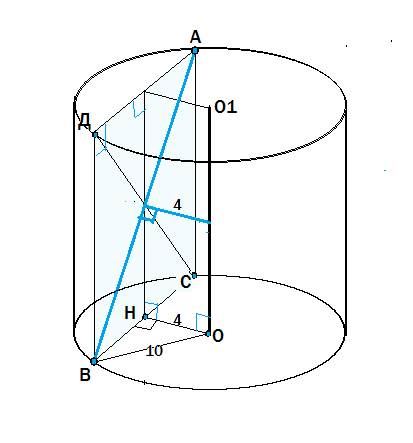
В равностороннем треугольнике все углы равны 60°.
Высоты, по свойству высоты равнобедренного треугольника, являются биссектрисами и медианами, и каждая делит его на 2 равных прямоугольных треугольника.
Высота в таких треугольниках является большим катетом, который противолежит углу 60°, сторона равностороннего треугольника- гипотенузой, а меньший катет противолежит углу 30° и равен половине гипотенузы (свойство)
-----------------
Примем меньший катет (половину стороны) равным а. Тогда гипотенуза (сторона равностороннего треугольника) равна 2а.
По т.Пифагора с²=a²+b² (с- гипотенуза, а и b- катеты)⇒
(2а)²=а²+((13√3)²⇒
3а²=13²•3 ⇒ а=13,
Сторона данного равностороннего треугольника 2а=26 (ед. длины)
или
с=b:sin60°, где с - сторона равностороннего треугольника, b- его высота.
с=(13√3):(√3/2)=26 (ед. длины)
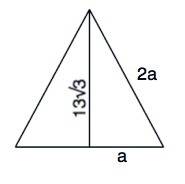
угол а=180-70-80=30град
сторона а=(b*sin80)/sin70 b=a*sin70/sin80=5*0,9397/0,9848=4,8
a^2=b^2+c^2-2bc*cos80
25=23,04+c^2-2*4,8*0,1736*c
c^2-1,7c=1,96
c=2,48