1. Знайдіть площу круга, якщо довжина кола 12π см.
2. На рисунку О – центр кола, ∠АВС = 21°. Знайдіть ∠AOC .
3. У трикутнику, периметр якого 118см, одна з сторін ділиться точкою дотику, вписаного в нього кола, на відрізки 21см і 15см. Найти две другие стороны.
----------------------------------
1.
С =2πR = 12π см -------------
S - ? S = πR² = (2πR)² /4π = C²/4π =(12π )² /4π = 36π (cм²)
2. Центральный угол ∠AOC = ◡ AC
вписанный угол ∠AOC = ◡ AC /2
∠AOC = 2*∠AOC =2*21° = 42°
3. Отрезки касательных, проведенных из одной точки, равны

ответ: 6√5 см
Объяснение:
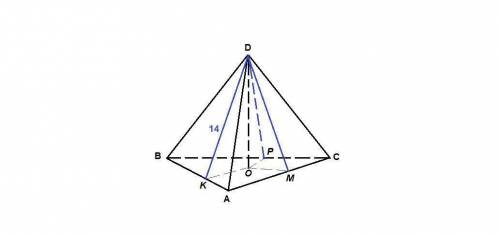
Пусть DO - высота пирамиды, DK, DM, DP - высоты боковых граней.
DK = DM = DP = 14 см по условию.
OK, OM и ОР - проекции наклонных, тогда они перпендикулярны сторонам треугольника АВС по теореме о трех перпендикулярах.
Если равны наклонные, проведенные из одной точки, то равны и их проекции, значит
ОК = ОМ = ОР, следовательно О - центр окружности, вписанной в ΔАВС, а ОК, ОМ и ОР - ее радиусы.
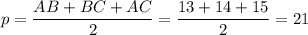
По формуле Герона
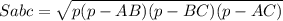
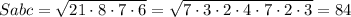 см²
см²
S = pr
84 = 21r
r = 4 см
ΔDKO: ∠DOK = 90°
по теореме Пифагора
DO = √(DK² - KO²) = √(196 - 16) = √180 = 6√5 см