Дано :
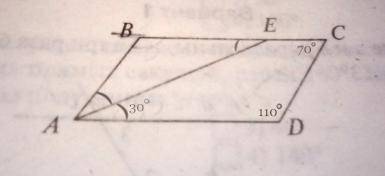
Четырёхугольник ABCD.
Отрезок АЕ - биссектриса ∠BAD.
∠EAD = 30°.
∠C = 70°.
∠D = 110°.
Найти :
∠В = ?
Рассмотрим прямые ВС и AD, которые пересечены секущей CD.
Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то эти прямые параллельны.∠С и ∠D - внутренние односторонние.
∠С + ∠D = 70° + 110° = 180°
Тогда по выше сказанному ВС ║ AD.
Рассмотрим эти же прямые, но тогда, когда они пересечены секущей АЕ.
При пересечении параллельных прямых секущей накрест лежащие углы равны.∠EAD и ∠ВЕА - накрест лежащие.
Тогда по выше сказанному -
∠EAD = ∠ВЕА = 30°.
Рассмотрим ΔАВЕ.
Биссектриса угла треугольника - это отрезок, который делит угол на два равных угла.То есть -
∠ВАЕ = ∠EAD = 30°.
Сумма внутренних углов треугольника равна 180°.Следовательно -
∠ВАЕ + ∠В + ∠EAD = 180°
∠В = 180° - ∠EAD - ∠ВАЕ
∠В = 180° - 30° - 30°
∠В = 120°.
120°.
Дано:
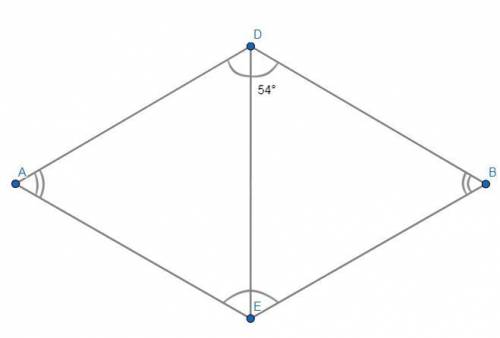
ADBE - ромб.
DE - диагональ.
∠EDB = 54°.
Найти:
∠ADB = ?
∠DBE = ?
∠BEA = ?
∠EAD = ?
1) Диагонали ромба являются биссектрисами углов, из которых они исходят. Поэтому, ∠ADB = 2*∠EDB = 2*54° = 108°.
2) Сумма двух углов параллелограмма (ромб - частный случай параллелограмма), прилежащих к одной стороне, равна 180°. Следовательно, ∠ADB+∠DBE = 180° ⇒ ∠DBE = 180°-∠ADB ⇒ ∠DBE = 180°-108° ⇒∠DBE = 72°.
3) Противоположные углы параллелограмма равны (на рисунке выделены дугами). Следовательно, ∠ADB = ∠BEA = 108°, ∠DBE = ∠EAD = 72°.
ответ: 108°, 72°, 108°, 72°.
R=abc\4S
S=√(р(р-а)(р-b)(h-c)=√(9*4*4*1)=√144=12 (ед²)
R=5*5*8\12*4=200\48=25\6=4 1\6 (ед.)
ответ: 4 1\6 ед.