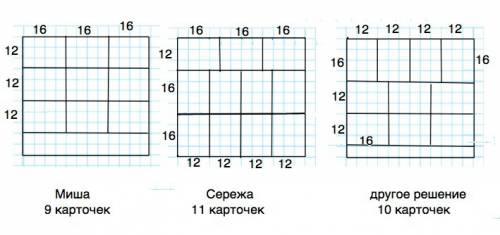
Длина картона кратна и ширине, и длине карточки:
48:16=3, 48:12=4. Ширина картона НЕ кратна ни длине, ни ширине карточки.
По ширине нужно разметить первую линию разреза так, чтобы оставшаяся часть картона по ширине была кратна одному из размеров карточки.
Если отрезать первую полосу шириной 16 см, ширина оставшейся части картона будет 28 - не кратна ни одному размеру карточки.
Следовательно, сначала нужно отрезать от картона полоску шириной в 12 см и разрезать на 3 части.
Оставшийся лист будет размером 32•48, и оба его размера теперь кратны длине карточки. Разрезав его по ширине на две полоски по 16 см, можно затем каждую разрезать на 4 карточки шириной 12 см, при этом излишков не образуется.
Если первую полоску отрезать шириной 16 см, ширина оставшейся части картона не будет кратной ни длине, ни ширине. Поэтому ее нельзя будет разрезать, чтобы не осталось лишнего картона.
Данный лист картона можно разрезать на 11 карточек, при этом не образуется излишков.
h=4,8 см
Объяснение:
1. диагонали ромба AC и BD
AC_|_BD
AC∩BD=O, AO=OC, BO=OD
2. пусть х, (x>0) -коэффициент пропорциональности ,тогда АС=4х см, ВD=3 х см
S ромба =(AC*BD)/2
24=(4x*3x)/2
6x²=24, x²=4, x=2 (x>0)
3. рассмотрим прямоугольный треугольник:
катет АО=(4*2)/2 - (1/2) АС, АО=4 см
катет ВО=(3*2)/2 -(1/2)BD, BO=3 см
гипотенуза АВ - сторона ромба, найти по теореме Пифагора:
AB²=AO²+BO²
AB²=4²+3², AB=5 см (или : катеты 4 и 3, => гипотенуза 5 -Пифагоров треугольник)
S ромба=AB*h, h - высота ромба
24=5*h
h=4,8
АМ² =(х+2)²+(у-5)²
ВМ²= (х-4)²+(у+3)².
Получим уравнение (х+2)²+(у-5)²+(х-4)²+(у+3)²=50.
После упрощения получим 2х²-4х+2у²-4у = -4.
х²-2х+у²-2у = -2. Выделим квадраты в левой части
х²-2х+1-1+у²-2у+1-1 = -2
(х-1)²+(у-1)² = 0. Это уравнение имеет единственное решение (1;1),т.к. сумма неотрицательных квадратов может быть равна 0, если каждое слагаемое равно 0.