1)
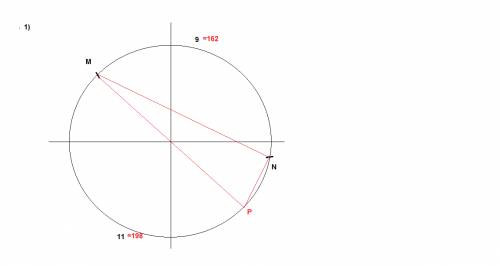
полная окружность 360 град ; 9/11 - всего 20 частей
дуга (9) = 9/20*360=162 град
дуга (11) =11/20*360=198 град
вершина N- лежит на окружности
сторона MP- совпадает с диагональю
свойство прямоугольного треугольника , вписанного в окружность
треугольник МNP - прямоугольный
<MNP=90 град
<MPN (вписанный)-опирается на дугу MN=162 град
свойство вписанного угла (он равен половине дуги, на которую опирается)
<MPN=1/2*162=81 град
<NMP=90- <NPM=90-81=9 град
ответ углы 90 ;81;9 град
1) S = 1/6
2) S = 1/2
3) S = 5/9
Объяснение:
Площадь треугольника можно вычислить по следующей формуле:
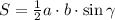
1) Обозначим площадь закрашенного ∆-ка S1 (см. рис.1)
Очевидно, т.к. точки делят стороны "единичного" ∆ка на равные отрезки, а угол 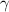 у единичного и у малого треугольника общий, то
у единичного и у малого треугольника общий, то
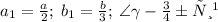
и площадь S1 равна
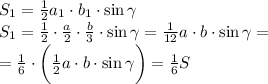
А т.к. 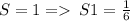
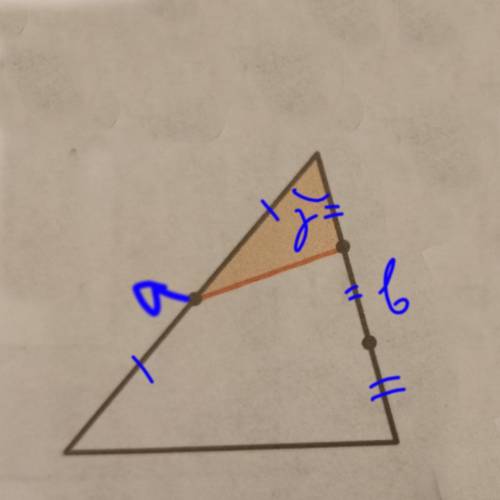
2) Пусть площадь закрашенной фигуры (а это - треугольник, см. рис.) равна S1.
Тогда площадь исходного единичного треугольника будет равна:
площадь S1, плюс общая площадь трех незакрашенных треугольников (обозначим их площади S2, S3, S4); а с учетом того, что площадь единичного треугольника равна 1:
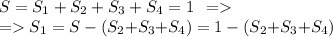
Треугольники 2, 3, 4 - образованы точно так же, как и треугольник в первой части задачи и соответственно их площади вычисляются точно так же:
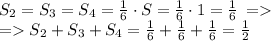
Соответственно, искомая площадь составляет
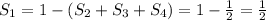
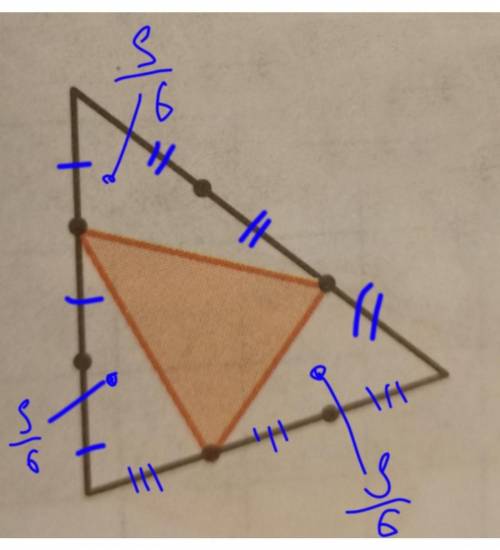
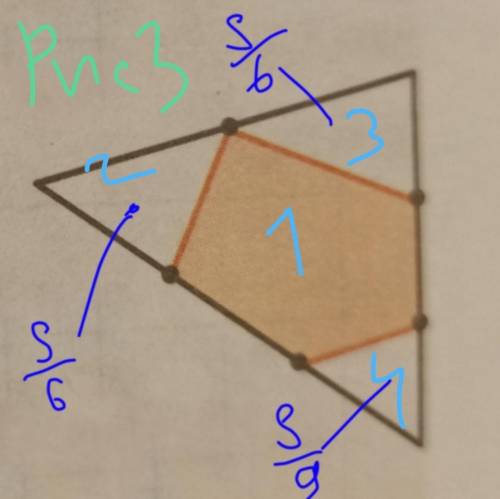
3) Пусть площадь закрашенной фигуры (а это - шестиугольник, см. рис.) равна S1
Тогда площадь исходного единичного треугольника будет равна:
площадь S1, плюс общая площадь трех незакрашенных треугольников (пусть их площади будут S2, S3, S4); а с учетом того, что площадь единичного треугольника равна 1:
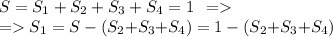
Площади треугольников 2, 3 - образованы точно так же, как и треугольник в первой части задачи и соответственно их площади вычисляются точно так же:
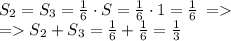
Но площадь треугольника 4 меньше: у него две стороны втрое меньше чем у исходного единичного, потому его площадь равна:
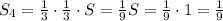
Следовательно, общая площадь незакрашенных частей равна:
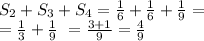
А искомая площадь закрашенной фигуры S1 составляет
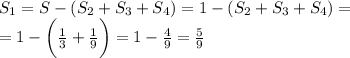
7