точки с координатами (-3.4) до оси Расстояние равно 4
Расстояние от точки до оси Оу будет не что иное как значение х, т.е. первое значение
№1:  . №2:
. №2: 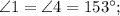
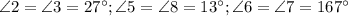 .
.
№1.
Пусть  , тогда
, тогда  - секущая.
- секущая.
Теорема: "При пересечении двух параллельных прямых секущей, сумма односторонних углов равна  .
.
 , по условию.
, по условию.
 и
и  - односторонние углы
- односторонние углы 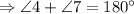
№2.
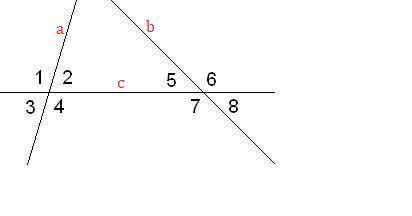
Обозначим данные прямые буквами 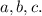
Пусть  - секущая прямых
- секущая прямых  и
и 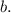
Теорема: "При пересечении двух параллельных прямых секущей, накрест лежащие углы равны".
 и
и 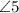 - накрест лежащие при пересечении
- накрест лежащие при пересечении  и
и  секущей
секущей  , однако
, однако 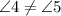 .
.

 и
и  - не параллельны.
- не параллельны.
============================================================
Свойство: "Вертикальные углы равны".
Свойство: "Сумма смежных углов равна  ".
".
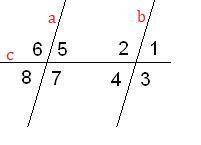
Рассмотрим углы, образовавшиеся при пересечении прямых  и
и 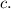
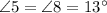 , по свойству вертикальных углов.
, по свойству вертикальных углов.
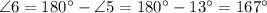 , по свойству смежных углов.
, по свойству смежных углов.
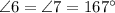 , по свойству вертикальных углов.
, по свойству вертикальных углов.
===========================================================
Рассмотрим углы, образовавшиеся при пересечении прямых  и
и  .
.
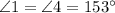 , по свойству вертикальных углов.
, по свойству вертикальных углов.
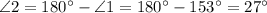 , по свойству смежных углов.
, по свойству смежных углов.
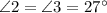 , по свойству вертикальных углов.
, по свойству вертикальных углов.
Объяснение:
Уравнение окружности имеет вид:
(x-x0)²+(y-y0)²=r²
Где (х0;у0) - координаты центра. r- радиус.
Подставив вместо х и у координаты данных точек получаем систему трех уравнений с тремя неизвестными:
для упрощения записи, вместо х0 напишу х, а вместо у0 напишу у:
(-3-x)²+y²=r²
(1-x)²+(3-y)²=r²
(5-x)²+y²=r²
вычтем из первого уравнения третье:
(-3-x)²-(5-x)²=0
9+6x+x²=25-10x+x²
16x=16
x=1
тогда получаем :
16+y²=r²
(3-y)²=r²
16+y²-(3-y)²=0
16+y²=9-6y+y²
6y=-7
y=-7/6
Тогда r²=820/49
Итак уравнение окружности имеет вид:
(x-1)²+(y+7/6)²=820/49
Расстояние от точки с координатами (-3.4) до оси Ох будет не что иное как значение у т.е. второе значение. Расстояние равно 4
Расстояние от точки до оси Оу будет не что иное как значение х, т.е. первое значение