
Противоположные стороны параллелограмма равны (свойство параллелограмма) => AB = CD, BC = AD,
Периметр равен сумме всех сторон, поскольку противоположные стороны равны, то периметр равен удвоенной сумме смежных сторон => P = 2(AB+BC) = 78см, 2(AB+BC) = 78см, AB+BC = 39см.
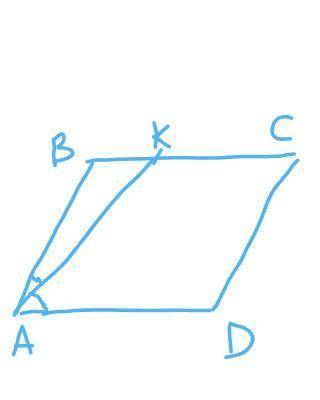
BK:KC = 3:7, BK = 3x, KC = 7x, BK + KC = 3x + 7x = 10x = BC.
Биссектрисса параллелограмма отсекает от него равнобедренный треугольник (свойство параллелограмма) => треуг. ABK — равнобедренный, AB = BK. =>
AB = BK = 3x,
AB + BC = 3x + 10x = 13x = 39см, x = 3см.
AB = 3x = 3 × 3см = 9см,
BC = 10x = 10 × 3см = 30см.
ответ: AB = 9см, BC = 30см, CD = 9см, AD = 30см.
ответ: Катети дорівнюють 24 і 10 см.
Объяснение:
Оскільки r (радіус вписаного кола) прямокутного трикутника обчислюється за формулою r=(a+b-c) /2, де a і b - катети, с - гіпотенуза, томи можемо отримати суму катетів (a+b) :
(a+b-c) /2=4 |2 (|2 означає, що ми множимо обидві частини рівняння на 2)
a+b-c=8
a+b=8+c=8+26=34 (з умови)
Також за теоремою Піфагора:
a^2+b^2=c^2 (^ це степінь)
Отримуємо систему рівнянь:
{a^2+b^2=26^2=676
{a+b=34
Розв'язуємо систему методом підстановки:
{a^2+b^2=26^2=676
{a=34-b
(34-b)^2+b^2=676
34^2-2*34*b+b^2+b^2=676
2×b^2-68b+1156-676=0
2×b^2-68b+480=0 |0,5
b^2-34b+240=0
Розв'язуємо квадратне рівняння:
D=34^2-4×1×240=1156-960=196=14^2
b1= (-(-34)+14)/2=(34+14)/2=24 см
b2= (-(-34)-14)/2=(34-14)/2=10 см
Відповідно, a1=34-24=10 см
a2=34-10=24 см
Отримуємо відповідь: катети дорівнюють 24 і 10см.