(х – а)² + (у – b)² = R² – уравнение окружности, записанное в общем виде, где (а; b) – координаты центра окружности; R – радиус окружности. Из условия задачи известно, что уравнение окружности проходит через точку 8 на оси Ox, то есть через точку с координатами (8; 0), и через точку 4 на оси Oy, то есть через точку с координатами (0; 4). При этом центр находится на оси Oy, значит, точка (0; b) является центром окружности. Подставляя поочередно координаты этих точек в уравнение, получим систему двух уравнений с двумя неизвестными:
(8 – 0)² + (0 – b)² = R² и (0 – 0)² + (4 – b)² = R²;
(8 – 0)² + (0 – b)² = (0 – 0)² + (4 – b)²;
8² + b² = (4 – b)²;
b² – 8 ∙ b + 4² – 8² – b² = 0;
8 ∙ b = – 48;
b = – 6, тогда, R = 10, и уравнение окружности примет вид:
х² + (у + 6)² = 10².
ответ: х² + (у + 6)² = 10² – уравнение данной окружности.
8 см - сторона многоугольника;
6 - количество сторон многоугольника.
Объяснение:
Радиус окружности вписанной в многоугольник является перпендикуляром к сторонам данного многоугольника.
Найдем длину стороны многоугольника:
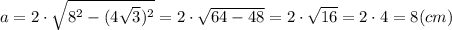
Если из центра окружности провести биссектрисы к углам многоугольника, то многоугольник будет разбит на равные равнобедренные треугольники.
Причем, длины сторон многоугольника равны проведенным биссектрисам (радиусу описанной окружности), т.к. R = 8 см и a = 8 см.
Т.е. многоугольник разбивается на равносторонние треугольники, у которых каждый угол равен 60°.
Найдем количество сторон многоугольника:
n = 360° : 60° = 6.
Проверим найденное количество сторон многоугольника через формулу:
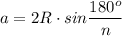
Подставив в формулу величину радиуса описанной окружности и найденное количество сторон многоугольника, должна быть получена длина стороны многоугольника, т.е. 8 см.
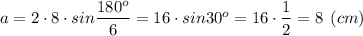
cos квадрат=1-sin квадрат= 9\ 41
tg= sin\cos= 40\9
ctg= 1\tg=9\40