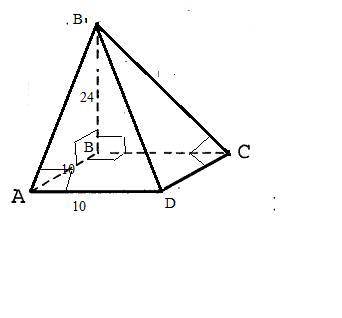
Основанием пирамиды является квадрат со стороной 10 см. Одно боковое ребро перпендикулярно плоскости основания и равно 24 см.
Вычисли площадь боковой поверхности.
Объяснение:
1)S(бок)=S(МВА)+S(МВС)+S(МАD)+S(МСD).
2)ΔМВА=ΔSМВС как прямоугольные по двум катетам⇒S(МВА)=S(МВС)=1/2*24*10=120 (см²).
Найдем МС= МА=√(24²+10²)=√676=26(см)
3)Т.к. прекция ВА⊥AD, то и наклонная МА⊥AD⇒ΔМAD-прямоугольный.
Т.к. прекция ВС⊥СD, то и наклонная МС⊥СD⇒ΔМСD-прямоугольный.
S(МАD)=S(МСD) как площади равных прямоугольных треугольников по катету и гипотенузе .
S(МАD)=S(МСD)=1/2*10*26=130 (см²)
4)S(бок)=2*120+2*130=500 (см²)
Объяснение:
Задача № 1.
Дано: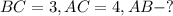 
Решение: Так как ABC - прямоугольный треугольник, то AB можно найти по теореме Пифагора:
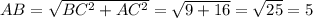
ответ: 5.
Задача № 2.
Дано: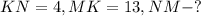 
Решение: Так как NMK - прямоугольный треугольник, то NK можно найти по теореме Пифагора:
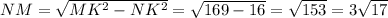
ответ: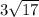 
Задача № 3.
Дано: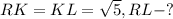 
Решение: так как RKL - прямоугольный треугольник, то RL найдем через теорему Пифагора:
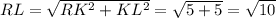
ответ: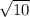 
Задача № 4.
Дано: ∠M = 30°,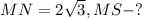 
Решение: MNS - прямоугольный треугольник:
1. Так как катет NS лежит напротив 30 градусов, то он равен половине гипотенузы:
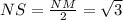
2. Найдем катет MS через теорему Пифагора:
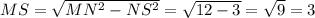
ответ: 3
Задача № 5.
Дано: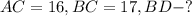 
Решение: Рассмотрим треугольник BDC - прямоугольный:
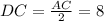- так как высота делит основание пополам в равнобедренном треугольнике
BD найдем по теореме Пифагора:
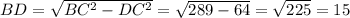
ответ: 15
Задача № 6.
Дано: ΔRMN - правильный,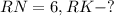 
Решение: Рассмотрим ΔRKN - прямоугольный:
1. Высота делит основание пополам в правильном треугольнике:
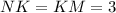
2. Найдем высоту по теореме Пифагора:
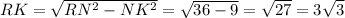
ответ: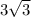 
Задача № 7.
Дано: ΔMPR - правильный,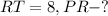 
Решение: Рассмотрим ΔPTR - прямоугольный:
1. Высота делит основание пополам, тогда:
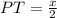
2. Найдем PR через теорему Пифагора:
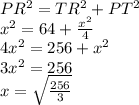
Отрицательный корень нам не подходит, так как длина отрезка не может быть отрицательной.
ответ: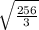 
Задание № 8.
Дано: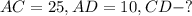 
Решение: Рассмотрим ΔACD - прямоугольный:
Найдем CD по теореме Пифагора:
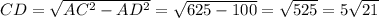
ответ: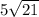 
35/7=30/6=15/x
35÷7=5
30÷6=5
15÷х=5
х=3
Третья сторона 3м