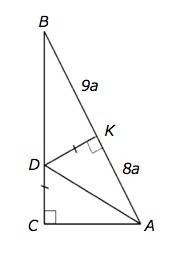
∆ АDК и АDС прямоугольные и равны по катету ( DС=DК -дано) и общей гипотенузе АD. ⇒
АК=АС и углы САD=КAD,⇒
АД - биссектриса угла ВАС.
Примем коэффициент отношения АК:КВ равным а. Тогда АВ=9а+8а=17а., АС=АК=8а
По т.Пифагора ВС=√(АВ²-АС²)=√225a²=15a
Периметр АВС=17а+15а+8а=40а
40а=80
а=2
СВ=30, АС=16, АВ=34 .
Биссектриса угла треугольника делит противолежащую углу сторону на отрезки, пропорциональные двум другим сторонам:
СД:ДВ=АС:АВ
Примем CD=х
х:(30-х)=16:34
34х=480-16х
50х=480
х=9,6 (ед. длины)
Медиана равнобедренного (и равностороннего) треугольника также является его высотой. Рассмотрим прямоугольный треугольник - гипотенуза в нем равна х (это сторона треугольника), один катет = 11√3 (это медиана), а второй катет = х/2, т.к. медиана делит сторону пополам.
По теореме Пифагора квадрат гипотенузы = сумме квадратов катетов:
х^/4 + 121*3 = x^
3/4x^ -363 =0
x^ = 484
x = 22 - сторона треугольника.