Признак равенства прямоугольных треугольников : Если гипотенуза и катет одного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие прямоугольные треугольники равны.
Объяснение:
Обозначим вторую точку пересечения ОВ с окружностью -Д.
∠ВАД и ∠ВСД-вписанные опираются на полуокружность( гр.мерой 180) , т.к. ВД диаметр .Значит они равняются половине дуги на которую опираются, т.е ∠ВАД =∠ВСД=90.
Прямоугольные треугольники ΔВАД= ΔВСД по катету и гипотенузе :гипотенуза ВД-общая, катеты АВ=ВС по условию.
Т.к. треугольники равны, то в равных треугольниках соответственные элементы равны: значит ∠1=∠2
V = 84 см³.
Объяснение:
Основание - параллелограмм. Стороны а и b. Диагонали D и d.
Одна из диагоналей (например, d) равна высоте параллелепипеда (дано).
Тогда имеем соотношения:
D·d = 39 см². a·d = 28 cм² и b·d = 17. =>
D = 39/d, a = 28/d и b = 17/d.
В параллелограмме углы, прилежащие к одной стороне, в сумме равны 180°. Заметим, что Sin(180-α) = Sinα.
По теореме косинусов для треугольника но диагонали D:
Cosα = ((28/d)² + (17/d)² - (39/d)²)/(2·(28/d)·(17/d) ≈ -0,470. (d² в числителе и знаменателе сокращаются).
Снова по теореме косинусов (теперь уже для треугольника на диагонали d c острым углом 180-α - по свойству углов параллелограмма):
d² = (28/d)² + (17/d)² - 2· (28/d)· (17/d)·0,470 =>
d^4 = 28²+17²-2·17·28·0,470 => d ≈ 5 см. => h = 5 см.
So = a·b·Sinα = 5,6·3,4·√(1 - 0,470²) ≈ 16,8 см².
Тогда V = So·h = 16,8·5 = 84 см³.
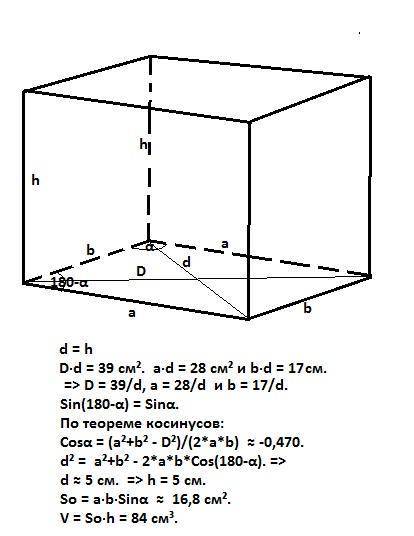
Рассмотрим прямоугольный треугольник я это лучше распишу на картинке. И площадь боковой поверхности тоже.