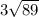
Объяснение:
Объём пирамиды:
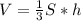, где S - площадь основания, h - высота пирамиды.
Значит 
У правильной четырёхугольной пирамиды основанием выступает квадрат. Если сторону квадрата обозначить как а, то S=a² ⇒ а=√S.
Боковое ребро пирамиды l, её высота h и полудиагональ основания образуют прямоугольный треугольник, в котором искомое ребро - гипотенуза, а высота и полудиагональ - катеты.
Диагональ квадрата равна √(2а²)=а*√2,
тогда половина диагонали равна а/√2, а так как а=√S,
то половина диагонали равна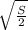 
Тогда, по теореме Пифагора:
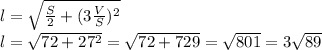
Объяснение:
1.
На любом луче, из его начала можно отложить отрезок заданной длины всего один. таким отрезком будет радиус. чтд
2.
Аналогично предыдущему только из центра окружности идут 2 луча.
3.
Отметим на окружности две произвольные точки A и B, соеденим их между собой хордой АВ и проведем из них отрезки в центр окружности АО и ВО. Эти отрезки будут радиусами окружности. равными между собой. Таким образом получим равнобедренный треугольник АОВ. Отметим точку М на середине отрезка АВ и проведем линию ОМ.
Так как АМ=ВМ и АОВ равнобедренный треугольник ОМ - медиана и одновременно высота (по св-ву высоты равноб тр-ка), то есть угол АМО - 90град. чтд
Площадь=8*4=32 см^2.