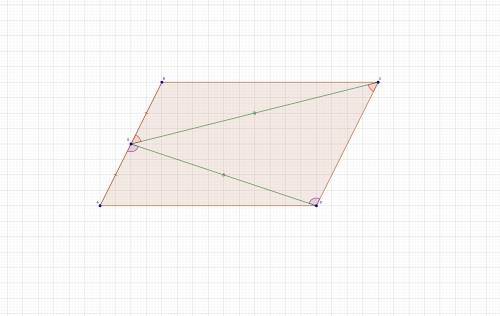
Доказательство:
Т.к. ABCD - параллелограмм, то AB//CD и AD//BC.
∠ECD = ∠CEB как накрест лежащие при параллельных прямых AB и CD и секущей EC.
∠EDC = ∠DEA как накрест лежащие при параллельных прямых AB и CD и секущей ED.
Т.к. EC = ED , то ΔECD - равнобедренный с основанием CD.
Значит ∠ECD = ∠EDC как углы при основании.
Следовательно ∠CEB = ∠DEA
ΔEBC = ΔEAD по двум сторонам и углу между ними (EB = EA по условию.)
См. рисунок 2.
Из равенства треугольников EBC и EAD следует, что ∠EBC = ∠EAD
и ∠BCE = ∠ADE
∠BCD = ∠BCE + ∠ECD
∠ADC = ∠ADE + ∠EDC
Следовательно ∠BCD = ∠ADC
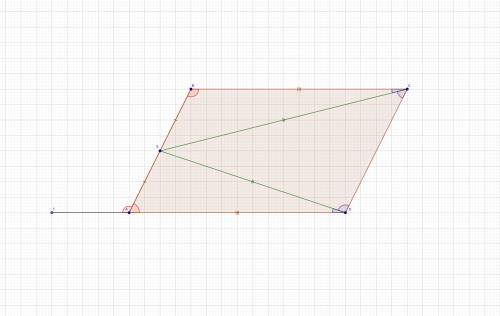
Продолжим сторону AD влево.
∠FAB = ∠ABC как накрест лежащие при параллельных прямых AD и BC и секущей AB.
∠FAB = ∠ADC как соответственные при параллельных прямых AB и DC и секущей AD
Собирая все вместе получаем, что ∠ABC = ∠BCD = ∠CDA = ∠DAB
Получается, что ABCD - параллелограмм в котором все углы равны. Следовательно ABCD - прямоугольник
сумма внешнего угла треугольника вместе с внутренним равна 180 градусов, поэтому внутренние углы в треугольнике равны 180-107=73градуса, 180-123=57 градусов. Сумма углов в треугольнике равна 180 градусов, поэтому третий угол равен
180-(73+57)=50 градусов. Внешний угол смежный с ним равен 180-50=130 градусов.
сумма внешних углов треугольника, взятых по одному около каждой вершины равна 360 градусов. 123+107+130=360градусов
2)внешний угол равен 88 градусов, значит внутренний угол равен 180-88=92градуса. так как этот угол тупой, то он является вершиной равнобедренного треугольника. Тогда углы при основании равны. По свойству внешнего угла их сумма равна внешнему углу, не смежному с ними, то есть 88 градусов. Каждый угол равен 88:2=44 градуса
180-30=150 градусов сумма двух углов (если бы они были равны)
150:2-75 градусов один угол
75+30=105 градусов второй угол
Удачи!