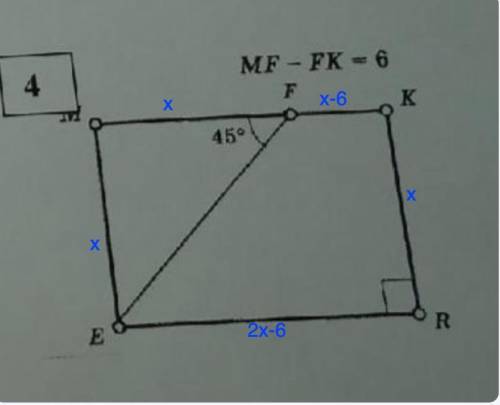
EM=KR=8; MK=ER=10
Объяснение:
Дано: ЕМКR - прямоугольник
∠MFE=45°
MF-FK=6
P (ЕМКR)=36
Найти: стороны прямоугольника.
Пусть MF=x ⇒ FK=MF-6=x-6
Рассмотрим ΔEMF - прямоугольный
∠MFE=45°
Сумма острых углов прямоугольного треугольника равна 90°.
⇒ ∠MEF=45°
ΔEMF - равнобедренный (углы при основании равны)
⇒ EM=MF=x
Противоположные стороны прямоугольника равны.
EM=KR=x
MK=ER=x+(x-6)=2x-6
Периметр прямоугольника равен удвоенной сумме длин соседних сторон.
Р (ЕМКR)=2(х+2х-6)=2(3х-6)
36=2(3х-6)
3х-6=18
3х=24
х=8
⇒ EM=KR=8
MK=ER=2x-6=10
Первый случай, все три прямые могут совпасть в одну не годится т.к. по условию есть пересекающиеся.
Второй случай, две прямые совпали, а третья их пересекает в одной точке, тогда 4 части.
Третий случай, все три прямые пересекаются в одной точке, тогда 6 частей.
Четвёртый случай, каждая прямая пересекает другие две в различных точках, тогда 7 частей.
Пятый случай, две прямые параллельные, а третья пересекает каждую из параллельных, тогда 6 частей.
Шестой случай, две прямые параллельные, а третья совпадает с одной из них не годится т.к. по условию есть пересекающиеся.
Седьмой случай когда все три прямые параллельны не годится т.к. по условию есть пересекающиеся.
ответ: на 4, 6 или 7 частей.
Объяснение:

BD пересекается с АС в точке О
АО=ОС=ВО=OD=6см
AB²=AO²+BO²-2AO*BO*sin45=36+36-2*36*√2/2=72-36√2≈72-50,4≈21,6
AB≈4,6
AD=√BD²-AB²=√144-21,6=√122,4≈11,1
S=AB*AD≈4,6*11,1≈50,9см²