С линейки проводим прямую и на ней с циркуля отложим отрезок АВ, равный отрезку МК. Для этого произвольно на прямой ставим точку А, с циркуля измеряем отрезок МК и строим окружность с центром в точке А радиуса МК (всю окружность строить необязательно, смотри, выделенное красным цветом). Точку пересечения окружности с прямой обозначаем В.
Далее строим угол ВАF равный углу 1. Для этого строим с циркуля окружность радиуса МК с центром в вершине угла 1 (всю окружность строить необязательно, смотри, выделенное красным цветом). Точки пересечения данной окружности со сторонами угла 1 обозначаем N и Р.
С циркуля измеряем длину отрезка NP и строим окружность радиуса NP с центром в точке В (всю окружность строить необязательно, смотри, выделенное синим цветом). Точку пересечения окружности с окружностью радиуса МК с центром в точке А обозначаем F.
Далее, проводим луч АF с линейки.
Далее, строим угол АВD равный углу 2. Для этого строим с циркуля окружность радиуса МК с центром в вершине угла 2 (всю окружность строить необязательно, смотри, выделенное красным цветом). Точки пересечения данной окружности со сторонами угла 2 обозначаем О и Е.
С циркуля строим окружность радиуса МК с центром в точке В (всю окружность строить необязательно, смотри, выделенное красным цветом), затем измеряем длину отрезка ОЕ и строим окружность радиуса ОЕ с центром в точке А (всю окружность строить необязательно, смотри, выделенное синим цветом). Точку пересечения данных окружностей обозначаем D.
Далее, проводим луч ВD с линейки.
Точку пересечения лучей АF и ВD обозначаем С. Получаем треугольник АВС, в котором по построению АВ = МК, ВАС =1, АВС =2, следовательно, треугольник АВС - искомый.
Данная задача не всегда имеет решение. Так как по теореме о сумме углов треугольника: сумма углов всякого треугольника равна 1800. Значит, сумма двух данных углов должна быть меньше 1800. Если же сумма двух данных углов будет больше 1800, то нельзя построить треугольник, углы которого равнялись бы данным углам.
Объяснение:
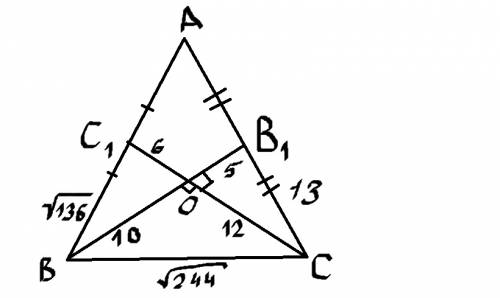
Задача решается проще, если вспомнить, что медианы в точке пересечения (т. е. все три медианы в любом треугольнике пересекаются внутри него строго в одной точке - это центр тяжести треугольника). Так вот эти медианы делятся в точке пересечения в соотношении 2 к 1, считая от вершины. Значит ВО=15*2/3=30/3=10 см, СО=18*2/3=6*2=12 см.
ОВ1=15/3=5 см, ОС1=18/3=6 см. Теперь нужно вспомнить теорему Пифагора. Треугольник ВОС - прямоугольный, значит ВС - гипотенуза.
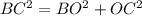
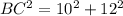
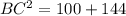
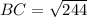
Треугольник ВОС1 - тоже прямоугольный, так как угол С1OB - прямой. Доказывается так.
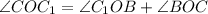
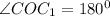 - как развернутый угол.
- как развернутый угол.
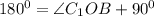
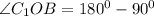
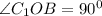
По теореме Пифагора из треугольника находим гипотенузу ВС1.
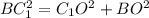
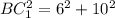
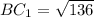
Заметим, что BC1 - половина АВ по определению медианы СС1.
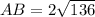
Треугольник B1OC - прямоугольный, так как угол B1OC - прямой, как вертикальный к углу С1OB. Та же теорема Пифагора, чтобы вычислить гипотенузу В1С.
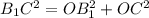
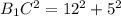
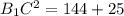
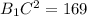
B1C=13 см.
Заметим также, что В1С - половина АС. Значит АС=26 см.
Вычислим периметр АВ.
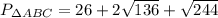
так как NK параллельно СА, то угол САК = углу AKN (как накрест лежащие)=39 градусов
Угол ANK= 180-39-39=102 градуса