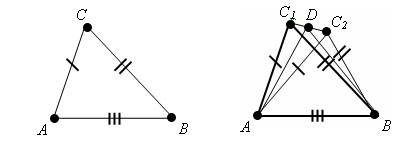
Дано:
∠A=∠A1
AB=A1B1
AC=A1C1
Доказать:
ΔABC=ΔA1B1C1
Доказательство:
Так как ∠А=∠А1 ( по условию), то треугольник АВС можно наложить на треугольник А1В1С1, так что вершина А совместится с вершиной А 1 , а стороны АВ и АС наложатся соответственно на лучи А1В1 и А1С1. Поскольку АВ = А1В1, АС = А1С1, то сторона АВ совместится со стороной А1В1, а сторона - АС состороной А1С1; в частности совместятся точки В и В1, С и С1. Следовательно, совместятся стороны ВС и В1С1. Итак, ∆АВС и ∆А1В1С1 полностью совместятся, значит они равны. как то такв середине треугольник не нужен
КМ - средняя линия основания.
SAKM - отсеченная пирамида.
Vsabc = 12
Vsabc = 1/3 Sabc · h
Vsakm = 1/3 Sakm · h, так как эти пирамиды имеют общую высоту.
Рассмотрим треугольники АВС и АКМ:
АК : АВ = 1 : 2
АМ : АС = 1 : 2
угол при вершине А общий, значит треугольники подобны по двум пропорциональным сторонам и углу между ними.
k = 1/2
Площади подобных треугольников относятся как квадрат коэффициента подобия:
Sakm : S abc = 1 : 4
Sakm = 1/4 Sabc
Vsakm = 1/3 · 1/4 Sabc · h = 1/4 (1/3 Sabc · h) = 1/4 Vsabc
Vsakm = 1/4 · 12 = 3