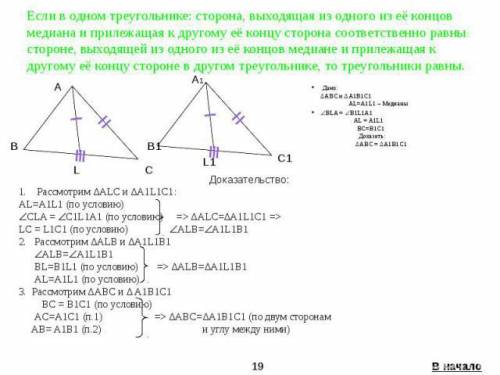
Из теоремы о касательной и секущих следует:
Теорема о секущих:
Если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть.
----------
Примем коэффициент отношения АЕ:ЕD равным а.
Тогда АЕ =2а, DE =7а
По теореме о секущих
CD•DE=AD•ED
(9+12)•12=(2a+7a)•7a
252=63a² ⇒ a²=4, a=2 ⇒
AE=4, ED=14, AD=18
Точка Е лежит на окружности, АС - диаметр, следовательно, угол CЕА, по свойству вписанного угла, опирающегося на диаметр, равен 90°⇒
СЕ - высота данного параллелограмма.
СЕ=√(CD²-DE²)=√(441-196)=7√5
Площадь параллелограмма равна произведению длин стороны и высоты, которая к ней проведена.
S=18•7√5=126√5 см²
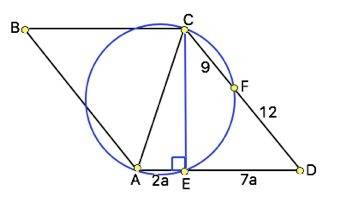
Теорема о секущих :
если из точки, лежащей вне окружности, проведены две секущие, то произведение одной секущей на её внешнюю часть равно произведению другой секущей на её внешнюю часть.
Примем коэффициент пропорциональности отрезков стороны параллелограмма за х.
Тогда получаем равенство 9х*7х = 21*3 = 63,
63х² = 63,
х² = 1,
х = √1 = 1.
Получаем длину стороны 9 см.
Отрезок СЕ будет высотой параллелограмма, так как АС - диаметр. а угол АЕС - прямой
Высоту находим по Пифагору:
Н = √(21² - 7²) = √(441 - 49) = √392 = 14√2 см.
Отсюда получаем площадь:
S = 9*14√2 = 126√2 ≈ 178,191 см².
Мы получаем два прямоугольных треугольника, у которых все три стороны равны:
АВ = ВС, т. к. треугольник равнобедренный по условию;
АН = НС, т. к. ВН - медиана;
ВН - общая сторона
По третьему признаку равенства треугольников (если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны) наши треугольники АВН и ВНС равны.