(26;4)
Объяснение:
Так как наши графики являются прямыми, функции выглядят так: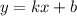 
Найдем значения k и b, подставив значения точек A и B в уравнение 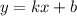и решив следующую систему:
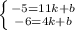
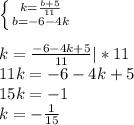
Найдем b, подставив в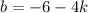 
:
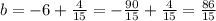
Первое уравнение имеет такой вид: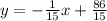 
- - - - - -
Найдем второе уравнение по аналогии (мне лень расписывать системами, так что я буду писать просто через новую строчку и в конце запишу итоговое решение системы)
- - - - -
- - - - -
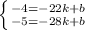
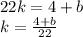
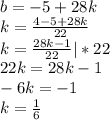
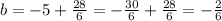
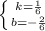
Второе уравнение имеет следующий вид: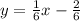 
Чтобы найти точку пересечения, нужно приравнять уравнения графиков.
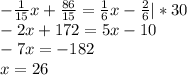
Чтобы найти y, нужно подставить в любое уравнение значение x.
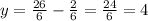
ответ: (26;4)
Найти площадь треугольника, координаты вершин которого А(-1;-7), В(3;1) и С(4;-13).
Есть несколько вариантов решения.
1) Прямо по координатам вершин по формуле:
Пусть точки A1(x1; y1), A2(x2; y2), A3(x3; y3) - вершины треугольника, тогда его площадь выражается формулой:
1/2 |x1-x3 y1-y3|
|x2-x3 y2-y3|
В правой части стоит определитель второго порядка. Площадь треугольника всегда положительна.
Решение. Принимая A за первую вершину, находим:
x1-x3 y1-y3
x2-x3 y2-y3 =
-1 - 4 -7 - (-13)
3 - 4 1 - (-13) =
-5 6
-1 14 = -5*14 - (-1)*6 = -64
По формуле получаем:S = (1/2)*|-64| = 32 кв. ед.
2) вышеприведенное решение - основано на векторном произведении.
Площадь равна половине модуля векторного произведения векторов
АВ и АС.
Находим векторы.
АВ = (3-(-1); 1-(-7)) = (4; 8)
АС = (4-(-1); -13-(-7)) = (5; -6).
Находим их векторное произведение с применением схемы Саррюса.
i j k| i j
4 8 0| 4 8
5 -6 0| 5 -6 = 0i + 0j - 24k - 0j - 0i - 40k = 0i + 0j - 64k.
Модуль равен √(0² + 0² + (-64)²) = 64.
Тогда площадь S = (1/2)*64 = 32 кв. ед.
3) Можно применить формулу Герона, предварительно определив длины сторон.
Координаты векторов сторон
АВ (c) BC (a) AС (b)
x y x y x y
4 8 1 -14 5 -6
Длины сторон АВ (с) = 16 64 80 = 8,94427191
BC (а) = 1 196 197 = 14,03566885
AC (b) = 25 36 61 = 7,810249676
Полупериметр р = 15,39509522
Площадь по Герону 15,39509522 6,450823307 1,359426369 7,584845541 = 32.
1
a=12 b=30
боковая сторона -с
с = (b-a) / (2sin<) = (30-12) / (2*0.8) =11.25
2
дуга/полная окружность 360 град
две дуги, градусные величины которых относятся как 3:7.<это 3+7=10 частей
дуга 3 3/10*360=108 <меньшая дуга
дуга 7 7/10*360=252
Под каким углом видна хорда из точки С, принадлежащей меньшей дуге окружности?
значит угол обзора<C опирается на большую дугу 252 град
<C -вписанный равен половине дуги 252/2=126 град
3
дуга/полная окружность 360 град
три дуги, градусные величины которых относятся как 3:10:11.<это 24 части
дуга 3 3/24*360=45 <меньшая дуга <напротив вписанный угол <C
<C -вписанный равен половине дуги 45/2=22,5 град = 22 град 30 мин
4
основания a= 40 b = 42
В окружность радиуса 29 вписана трапеция , значит равнобедренная
центр окружности лежит вне трапеции. - пусть точка О
образуется два равнобедренных треугольника с вершиной в т.О и основаниями a , b
боковые стороны в треугольниках -радиусы R=29
по теореме Пифагора
высота треугольника 1
h1^2 = R^2- (a/2)^2 ; h1 = √ (R^2- (a/2)^2 )
высота треугольника 2
h2^2 = R^2- (b/2)^2 ; h1 = √ (R^2- (b/2)^2 )
значит высота трапеции
H = h1 - h2 = √ (R^2- (a/2)^2 ) - √ (R^2- (b/2)^2 ) <подставим числа
H = √ (29^2- (40/2)^2 ) - √ (29^2- (42/2)^2 ) = 1