Дана окружность и точки X и Y внутри нее.
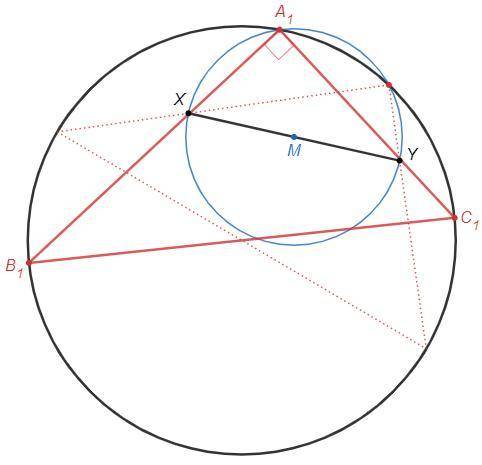
На отрезке XY как на диаметре построим окружность. Пересечения построенной окружности с данной окружностью - вершины треугольника (A1, A2).
Объяснение:
1) Построим середину отрезка XY - точку M.
(Для этого построим серединный перпендикуляр к отрезку:
- две дуги с центрами в концах отрезка
- прямую через точки пересечения дуг
Прямая пересечет отрезок в его середине)
Серединный перпендикуляр к отрезку - ГМТ, равноудаленных от двух точек.
2) Построим окружность с центром M радиусом MX.
Пересечение построенной окружности с данной окружностью - вершина А1 искомого треугольника.
Вписанный угол A1 - прямой, т.к. опирается на диаметр XY.
Окружность - ГМТ, из которых данный отрезок (диаметр) виден под прямым углом.
3) Проведем прямые A1X и A1Y. Их пересечения с данной окружностью - вершины B1 и С1 искомого треугольника.
Аналогично строим вершины B2 и С2, если имеется точка A2.
ответ: 16 см, 30 см.