Выпуклый многоугольник называется правильным, если равны все его стороны и равны все его углы.
Сумма внешних углов выпуклого многоугольника равна 360°.
Угол А1А8К - развернутый, равен 180°
Данный многоугольник правильный, все его внутренние, а, значит, и внешние углы равны.
Угол А7А8К=360°:8=45°⇒
угол А1А8А7=180°- 45°=135°
∆ А1А8А7 - равнобедренный.
∠А1А7А8=А7А1А8=(180°-135°):2=22,5°
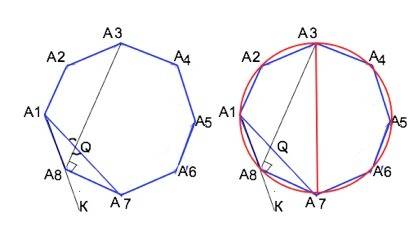
А3А7 - диаметр описанной окружности.⇒ ∠А3А8А7=90°
Сумма острых углов прямоугольного треугольника равна 90° ⇒
∠А7QА8=90°-22,5°=67,5°
Угол А1QА3 =углу А7QА8 как вертикальный
Угол А1QА =67,5°
Пусть точка пересечения биссектрисы и ВС будет Н,
угол ВНА=углу НАД (как накрест лежащие),
значит угол А = 35*2=70 градусам
Угол С также равен углу А и = 70 градусам (по признаку параллелограмма)
а угол В= углу Д = 180 градусов - 70градусов = 110 градусам.