5) Периметр квадрата со стороной AM равен 4AM.
4AM=2BC <=> AM=BC/2
Отрезок из прямого угла к гипотенузе, равный ее половине - медиана.
AM - медиана и высота, следовательно △ABC - равнобедренный, острые углы 45.
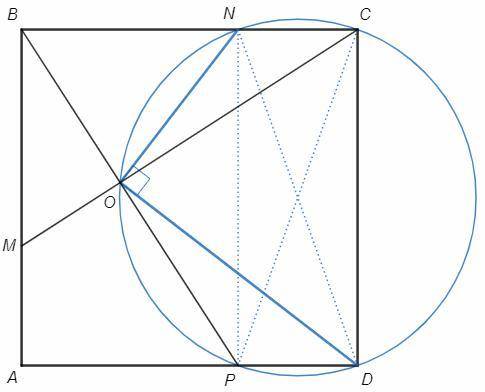
6) Продолжим перпендикуляр BO до пересечения с AD в точке P.
OBM= 90-OMB =BCM
△ABP=△BCM (по катету и острому углу)
AP=BM=BN => PD=NC
PNCD - прямоугольник, диагонали являются диаметрами описанной окружности.
COP=90, точка O лежит на окружности с диаметром CP.
Вписанный угол NOD опирается на диаметр ND, NOD=90
1) Так как у ромба острые углы равны по 60 градусов, то равнобедренные тр-ки ДАВ и ВСД (ДА=АВ=ВС=СД) являются равносторонними (углы при оновании равны по (180-60)/2=60 градусов. Тогда диагональ ВД равна сторонам ромба пусть они равны по х).
2) Рассмотрим чет-ник DFKO: DO=1/2*DB=x/2; DF=DC/2=x/2; FK=DB/2=x/2 (сред. линия тр-ка ДВС); ОК=ДС/2=х/2 (сред. линия тр-ка ДВС). Итак, стороны 4-хугольника равны, значит это ромб, а по свойствам ромба: диагонали его взаимно перпендикулярны, ч.т.д.