30 см
Объяснение:
Рассмотрим вложение.
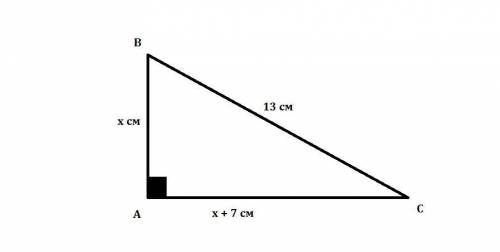
Нам дан ΔАВС: ∠А = 90°, ВС = 13 см
Пусть АВ = х см, тогда АС = х + 7 см. Воспользуемся т.Пифагора для нахождения стороны.
АВ² + АС² = ВС²
х² + (х + 7)² = 13²
х² + х² + 14х + 49 = 169
2х² + 14х + 49 - 169 = 0
2х² + 14х - 120 = 0 |:2
х² + 7х - 60 = 0
D = 7² - 4 * (-60) = 49 + 240 = 289 = 17²
x₁ = (-7 - 17)/2 = -24/2 = -12
x₂ = (-7 + 17)/2 = 10/2 = 5
т.к. сторона не может быть отрицательна, то АВ = 5 см, тогда
АС = 5 + 7 = 12 см
Чтобы найти периметр треугольника, надо сложить все стороны.
Р = АВ + ВС + АС = 5 + 13 + 12 = 30 см
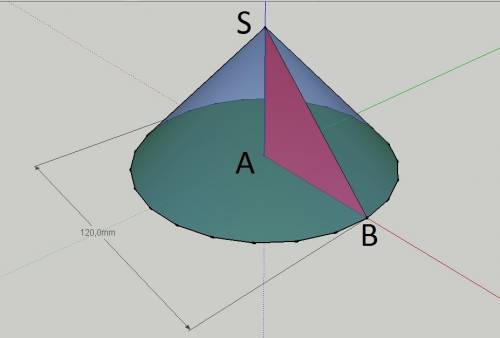
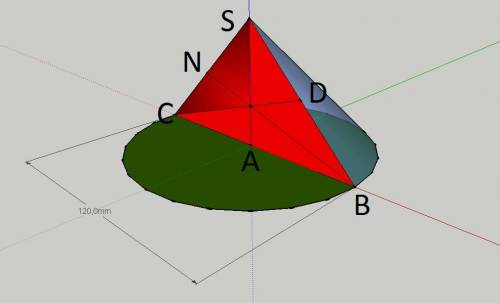
Рассмотрим треугольник АВS, который является частью (половиной) осевого сечения конуса. Сторона АВ явлется радиусом основания конуса. Rк = Dк / 2 = 12см / 2 = 6см; По условию угол ASB = 60°, тогда осевое сечение конуса представляет собой равносторонний треугольник CSB в котором SA - высота, медиана и биссектриса, проведенные из точки S к стороне АВ; CD - высота, медиана и биссектриса, проведенные из точки С к стороне BS; BN - высота, медиана и биссектриса, проведенные из точки В к стороне CS. Отсюда SA = CD = BN = CB √3 / 2 = 12см * 1,73 / 2 = 10,38 см. Rосн = 6см; высота AS = 10,38 см.
треугольник АОД и ВОС подовно
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
AD/BC=4/3
H=4/3*h
высота H+h=7
S=(AD+BC)/2*7=24.5