Sabcd ≈ 7,5 ед.
Объяснение:
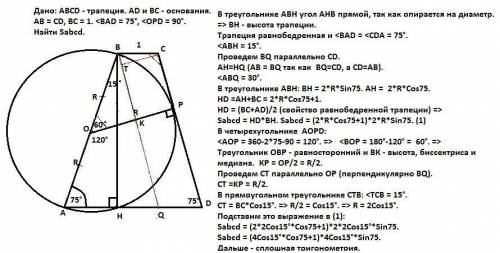
В треугольнике АВН угол АНВ прямой, так как опирается на диаметр. => ВН - высота трапеции.
Трапеция равнобедренная и <BAD = <СDА = 75°. <ABH = 15°.
Проведем BQ параллельно CD.
AH=HQ (АВ = BQ так как BQ=CD, a CD=AB). <ABQ = 30°.
В треугольнике АВН:
BH = 2*R*Sin75. АН = 2*R*Cos75. HD =AH+BC = 2*R*Cos75+1.
HD = (BC+AD)/2 (свойство равнобедренной трапеции) =>
Sabcd = HD*BH.
Sabcd = (2*R*Cos75+1)*2*R*Sin75. (1)
В четырехугольнике АОРD: <AOP = 360-2*75-90 = 120°. =>
<BOP = 180°-120° = 60°. =>
Треугольник ОВР - равносторонний и ВК - высота, биссектриса и медиана. КР = ОР/2 = R/2.
Проведем СТ параллельно ОР (перпендикулярно BQ).
CT =KP = R/2.
В прямоугольном треугольнике СТВ: <TCB = 15°.
СТ = ВС*Cos15°. => R/2 = Cos15°. => R = 2Cos15°.
Подставим это выражение в (1):
Sabcd = (2*2Cos15°*Cos75+1)*2*2Cos15°*Sin75.
Sabcd = (4Cos15°*Cos75+1)*4Cos15°*Sin75.
Дальше - сплошная тригонометрия.
Но подставив табличные значения, получим Sabcd ≈ 7,5 ед.
Если надо AD = AH+HD = 2RCos75+2RCos75+1 =
8Cos15*Cos75 +1 ≈ 3 ед.
Проведем ОК ⊥ СВ и соединим точки Р и К. По теореме о трех перпендикулярах: РК ⊥ СВ. РК — высота треугольника ВРС. Sсеч = SBPC=1/2 CB*PK. ВС=г.
CB = r корень из 2. PK = корень из L^2 - (r/2)^2 = корень из (2L^2 - r^2) / корень из 2. S сечения = 1/2*r* корень из (2L^2 - r^2) / корень из 2= r/2 * 2L^2 - r^2