Дан равнобедренный треугольник ABC ( AB = BC ).
Биссектриса AE пересекает высоту BD в точке О, причем OB/OD=3/1 .
Пусть АВ = ВС = х, АD = DC = y.
Используем свойство точки пересечения биссектрис.
Каждая биссектриса треугольника делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины.
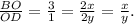
Отсюда следует х = 3у.
По Пифагору х² = у² + (3 + 1)². Зваменим у.
(3у)² = у² + 4²,
8у² = 16,
у = √(16/8) = √2.
Переходим к углам.
Угол OAD = ABD как взаимно перпендикулярный.
tg OAD = tg ABD = √2/4.
Находим ОК = AD*tg OAD = √2*(√2/4) = 2/4 = 0.5.
Отрезок ВК = 4 - 0,5 = 3,5.
ответ: ВК/KD = 3,5/0,5 = 7/1.

Стороны равны: 2 см; 4,5 см; 2 см; 4,5 см;
углы равны: 64°; 116°; 64°; 116°.
Объяснение:
Задание
Диагонали четырехугольника равны 4 см и 9 см, а угол между ними равен 64°. Найдите стороны и углы четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Решение
Согласно теореме Вариньона, середины сторон произвольного четырёхугольника являются вершинами параллелограмма.
Так как полученный четырёхугольник является параллелограммом Вариньона, то:
1) его противоположные стороны попарно равны и равны 1/2 соответствующей диагонали:
АВ = СD = 4 : 2 = 2 см
ВС = AD = 9 : 2 = 4,5 см;
2) углы между сторонами параллелограмма Вариньона равны углам между диагоналями исходного четырёхугольника:
∠DAB = ∠DCB = 64°
∠ABC = ∠ADC = 180°-64° = 116°
стороны равны: 2 см; 4,5 см; 2 см; 4,5 см;
углы равны: 64°; 116°; 64°; 116°.
Так как медиана разбивает треугольник на два равновеликих треугольника, то площадь `S_1` треугольника АСМ равна половине площади `S` треугольника АВС
Обозначим `BC=a`, `AC=b`, `/_DCB=alpha`, тогда `S_1=1/2*a/2*9*sinalpha +1/2*b*9*sinalpha=9/2*sinalpha*(a/2+b)`. Аналогично `S=1/2*14*sinalpha*(a+b)`. Так как `S=2S_1`, то `a:b=4:5` и `a=4/5*b`. Отсюда `AB=3/5*b`. По свойству биссектрисы внутреннего угла треугольника `BD : DA=4:5`, поэтому можно положить `BD=4x`, `DA=5x`. Тогда `AB=9x`, `b=15x`, `a=12x`. Так как `14^2=(12x)^2+(4x)^2`, то `x^2=196/160=49/40`. Отсюда площадь треугольника АВС равна `1/2*9x*12x=(1323)/(20)`
ответ:`(1323)/(20)