S=117 см²
Объяснение:
так в задании: "Края основания прямоугольного параллелепипеда составляют 12 см и 5 см. Длина боковой стороны ребра 9 см. Рассчитайте площадь сечения диагонали!"
предположу, что условие должно быть таким:
стороны основания прямоугольного параллелепипеда 12 см и 5 см. длина бокового ребра 9 см. найти площадь диагонального сечения прямоугольного параллелепипеда
диагональное сечение прямоугольного параллелепипеда - прямоугольник со сторонами d - диагональ основания прямоугольного параллелепипеда и h - высота прямоугольного параллелепипеда - длина бокового ребра
рассмотрим прямоугольный треугольник:
катет а=12 см - сторона основания параллелепипеда
катет b =5 см - сторона основания параллелепипеда
гипотенуза d - диагональ основания параллелепипеда, найти по теореме Пифагора:
d²=a²+b², d²=12²+5², d=13 см
найдем площадь сечения: S=d*h
S=13*9, S=117 см²
Будем пользоваться теоремой о биссектрисе.
Она заключается в следующем: отношение сторон треугольника, содержащихся в угле, из которого проведена биссектриса, равна отношению отрезков, на которые делит биссектриса противолежащую сторону.
Назовем точку пересечения MN и биссектрисы AK через R; Тогда из данного в условии легко вывести, что биссектриса угла C проходит через R. Пусть RC ∩ AB = F; Пусть AM=2x, MB=x. Тогда x=2; По теореме Менелая для треугольника AMN: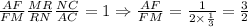 
, ну а отсюда легко получить AF=2,4 и FM=1,6; Значит BF=3,6 и AF=2,4; По вышеизложенной теореме о биссектрисе имеем: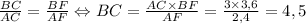 
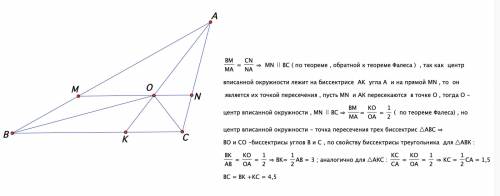
СД - диаметр окружности
АВ _|_ СД
АВ пересекается с СД в точке М
О - центр окружности
СМ:МД=25:1
х - коэффициент пропорциональности
СМ=25 х, СД=1 х
СД=26 х, тогда R=13 х
ОМ=12 х
прямоугольный ΔАМО: АМ=15 см (30:2=15), ОМ=12х, ОА=13х
по теореме Пифагора:
(13х²)=15²+(12х)², 169х²=225+144х². 25х²=225. 5х=15. х=5
R=13*5=65
R=65 см